目录
快速导航-
课程教材教法 | 整体观念下小初衔接数学教学的实践
课程教材教法 | 整体观念下小初衔接数学教学的实践
-
课程教材教法 | 实验性学习让数学课堂“生”动起来
课程教材教法 | 实验性学习让数学课堂“生”动起来
-

课程教材教法 | 单元视域下的章节起始课教学探析
课程教材教法 | 单元视域下的章节起始课教学探析
-

课例评析 | 核心素养导向下的初中几何实验教学实践研究
课例评析 | 核心素养导向下的初中几何实验教学实践研究
-
课例评析 | 素养本位的初中数学大单元教学设计框架和模式研究
课例评析 | 素养本位的初中数学大单元教学设计框架和模式研究
-

课例评析 | 构造基本图形 凸显几何直观
课例评析 | 构造基本图形 凸显几何直观
-

课例评析 | 基于主体参与的初中数学单元复习教学实践研究
课例评析 | 基于主体参与的初中数学单元复习教学实践研究
-

教学实践 | HPM视域下数学史渗透措施的研究
教学实践 | HPM视域下数学史渗透措施的研究
-

教学实践 | 关注几何直观 厚植模型思想
教学实践 | 关注几何直观 厚植模型思想
-

教学实践 | 多样学习方式:助推学习力提升
教学实践 | 多样学习方式:助推学习力提升
-
教学实践 | “生本”理念下的习题课探究
教学实践 | “生本”理念下的习题课探究
-
教学实践 | 核心素养导向下基于“数学思维”发展的教学实践与探索
教学实践 | 核心素养导向下基于“数学思维”发展的教学实践与探索
-

教学实践 | 新旧联系促思维 师生合作共成长
教学实践 | 新旧联系促思维 师生合作共成长
-

教学实践 | 基于运算能力培养的初中数学教学策略研究
教学实践 | 基于运算能力培养的初中数学教学策略研究
-

教学实践 | 基于深度交流的初中数学教学设计
教学实践 | 基于深度交流的初中数学教学设计
-

教学实践 | 立足微专题教学 提升数学解题能力
教学实践 | 立足微专题教学 提升数学解题能力
-

教学实践 | 单元整体视域下的章起始课教学实践与探索
教学实践 | 单元整体视域下的章起始课教学实践与探索
-
教学实践 | 聚焦复习教学 发展核心素养
教学实践 | 聚焦复习教学 发展核心素养
-
教学实践 | 数学类比法在平面几何教学中的应用研究
教学实践 | 数学类比法在平面几何教学中的应用研究
-
教学实践 | 核心素养背景下初中数学渗透数学文化的策略研究
教学实践 | 核心素养背景下初中数学渗透数学文化的策略研究
-

教研在线 | 提高数学中考复习效率的策略研究
教研在线 | 提高数学中考复习效率的策略研究
-
教研在线 | 初中数学教材插图之功能挖掘
教研在线 | 初中数学教材插图之功能挖掘
-
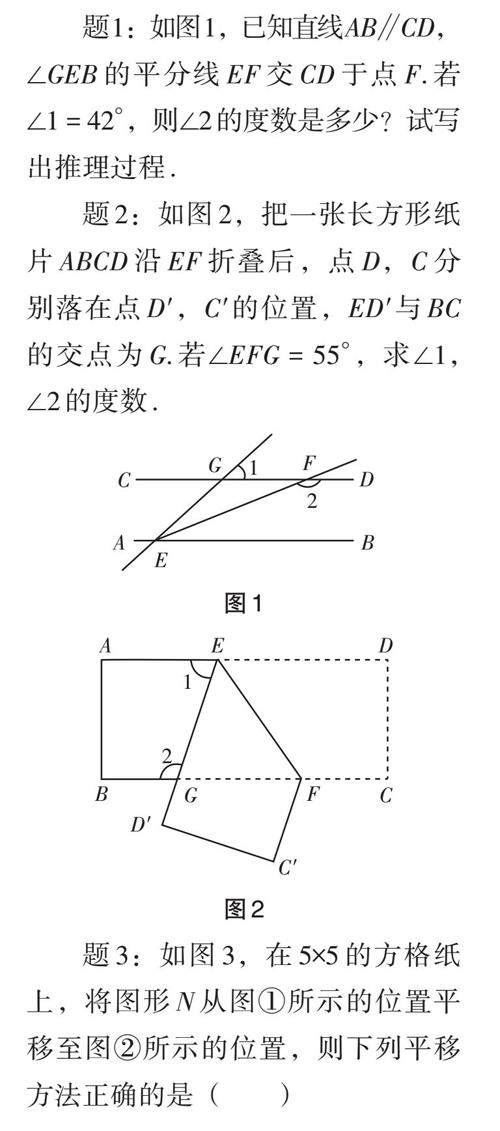
教研在线 | 核心素养导向下的初中数学作业设计的理念与策略探索
教研在线 | 核心素养导向下的初中数学作业设计的理念与策略探索
-

教研在线 | 初中数学教学中跨学科融合的实践研究
教研在线 | 初中数学教学中跨学科融合的实践研究
-

问题探索 | 问题驱动式教学的实践与研究
问题探索 | 问题驱动式教学的实践与研究
-

问题探索 | 回归原点 探寻本质 发展素养
问题探索 | 回归原点 探寻本质 发展素养
-
问题探索 | “精准预习演练教学”模式的实践与思考
问题探索 | “精准预习演练教学”模式的实践与思考
-

问题探索 | 核心素养背景下数学讲评课教学的探索与研究
问题探索 | 核心素养背景下数学讲评课教学的探索与研究
-
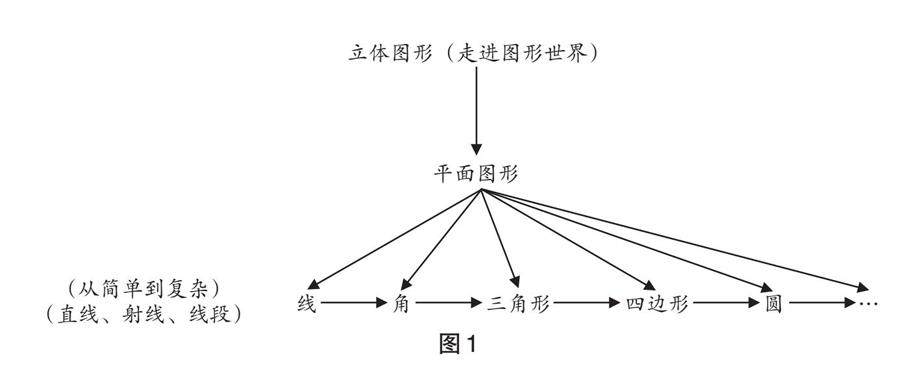
教学技巧 | 核心素养背景下单元教学设计研究
教学技巧 | 核心素养背景下单元教学设计研究
-

教学技巧 | 聚焦概念教学 发展核心素养
教学技巧 | 聚焦概念教学 发展核心素养
-
教学技巧 | 立足数学课堂 促进思维发展
教学技巧 | 立足数学课堂 促进思维发展























 登录
登录