目录
快速导航-
课程教材教法 | “课程思政”视域下的高中数学教学探索与实践
课程教材教法 | “课程思政”视域下的高中数学教学探索与实践
-
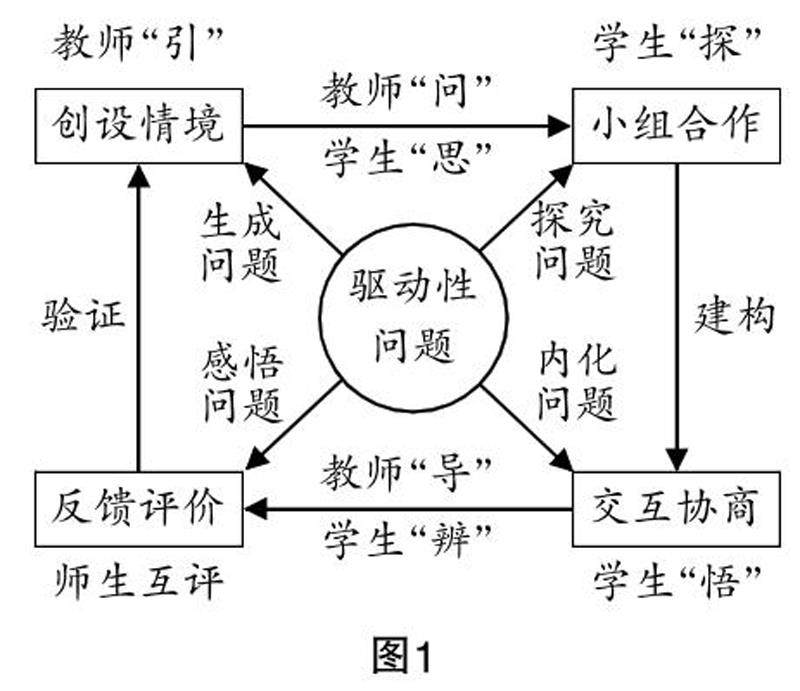
课程教材教法 | PBL教学模式下高中统计教学的探索与实践
课程教材教法 | PBL教学模式下高中统计教学的探索与实践
-

课程教材教法 | “三新”背景下的高中数学教学困境与应对措施
课程教材教法 | “三新”背景下的高中数学教学困境与应对措施
-

课例评析 | 跨学科项目式学习视域下的高中数学建模教学
课例评析 | 跨学科项目式学习视域下的高中数学建模教学
-

课例评析 | 类比视角下的概念教学应突出“生本”理念
课例评析 | 类比视角下的概念教学应突出“生本”理念
-

课例评析 | 从不同教材编写思路中挖掘核心素养的生长点
课例评析 | 从不同教材编写思路中挖掘核心素养的生长点
-

课例评析 | 基于“课堂深度学习”的高中数学教学实践研究
课例评析 | 基于“课堂深度学习”的高中数学教学实践研究
-

课例评析 | “生本”理念下的微专题复习课探究
课例评析 | “生本”理念下的微专题复习课探究
-
教学实践 | 聚焦概念教学 发展核心素养
教学实践 | 聚焦概念教学 发展核心素养
-

教学实践 | 立足基础 经历生成 探究本质
教学实践 | 立足基础 经历生成 探究本质
-
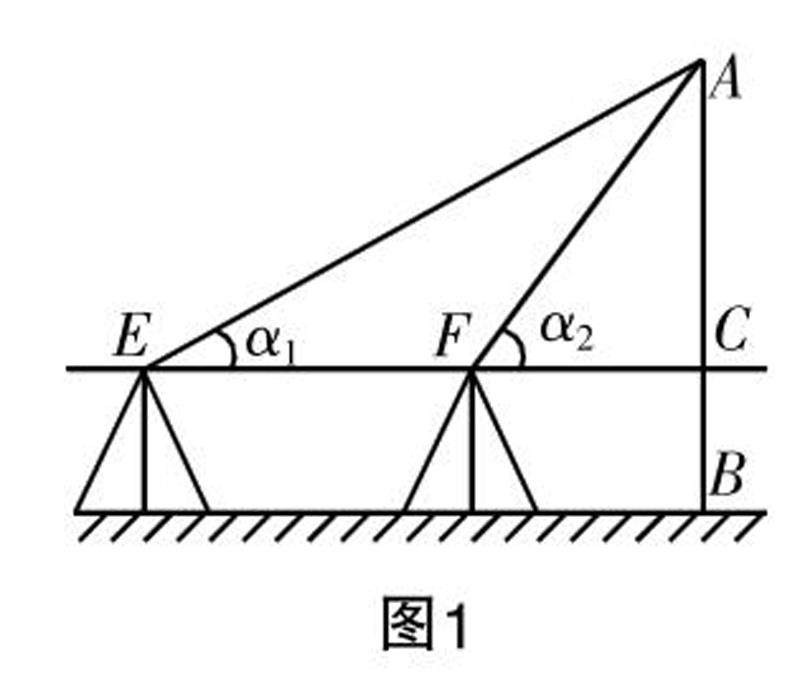
教学实践 | 基于深度学习的高中数学STEM项目设计
教学实践 | 基于深度学习的高中数学STEM项目设计
-
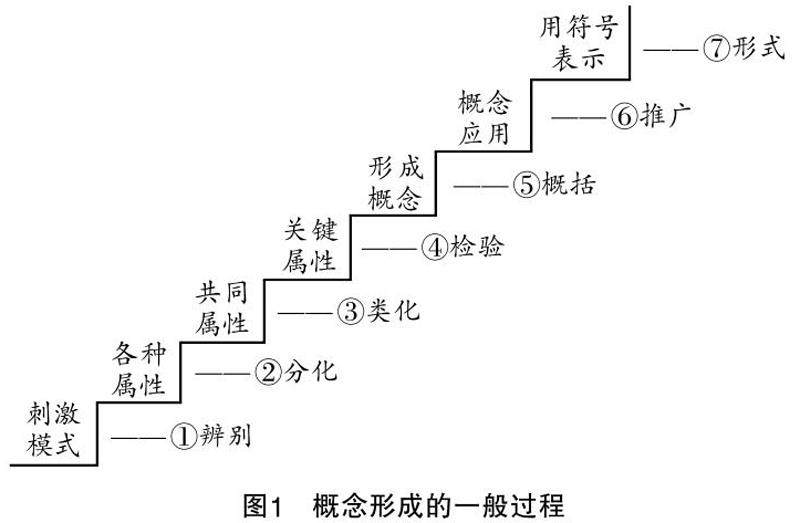
教学实践 | 理解数学视角下的高中数学概念教学
教学实践 | 理解数学视角下的高中数学概念教学
-

教学实践 | 问题引领促生成 深度探究促发展
教学实践 | 问题引领促生成 深度探究促发展
-

教学实践 | 浅谈探究性教学在高中数学教学中的应用研究
教学实践 | 浅谈探究性教学在高中数学教学中的应用研究
-

教学实践 | 关注学习体验 发展运算素养
教学实践 | 关注学习体验 发展运算素养
-

教学实践 | 单元整体视域下追求自然发展的课堂探索与研究
教学实践 | 单元整体视域下追求自然发展的课堂探索与研究
-
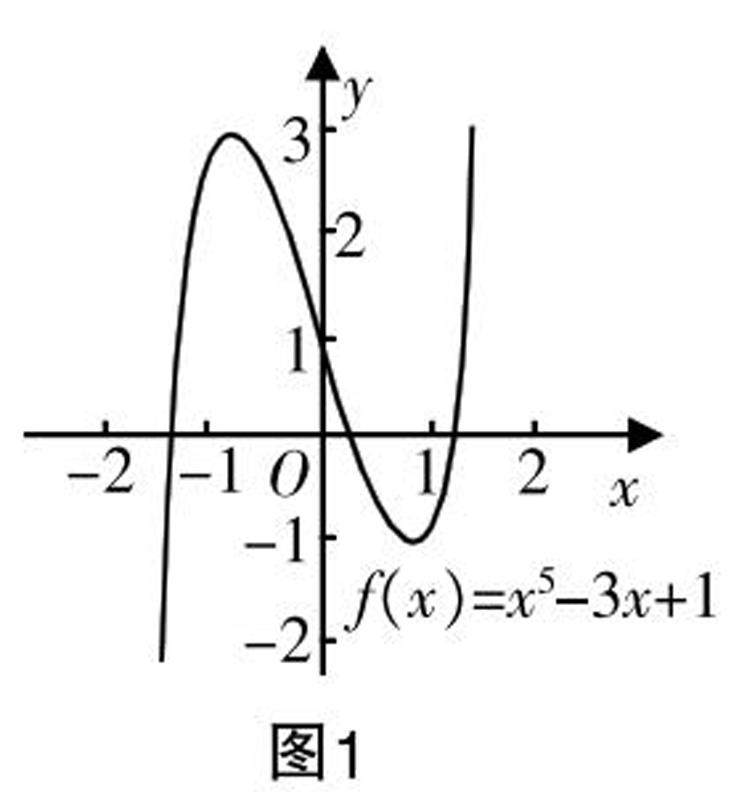
教学实践 | 聚焦单元主题 关注学习能力
教学实践 | 聚焦单元主题 关注学习能力
-

教学实践 | 基于深度学习的“问题导向式教学”的实践探索
教学实践 | 基于深度学习的“问题导向式教学”的实践探索
-
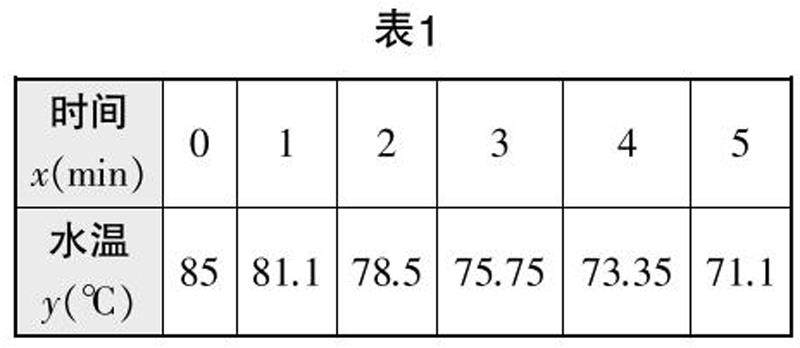
教学实践 | 跨学科项目式学习视域下的高中数学建模教学1
教学实践 | 跨学科项目式学习视域下的高中数学建模教学1
-
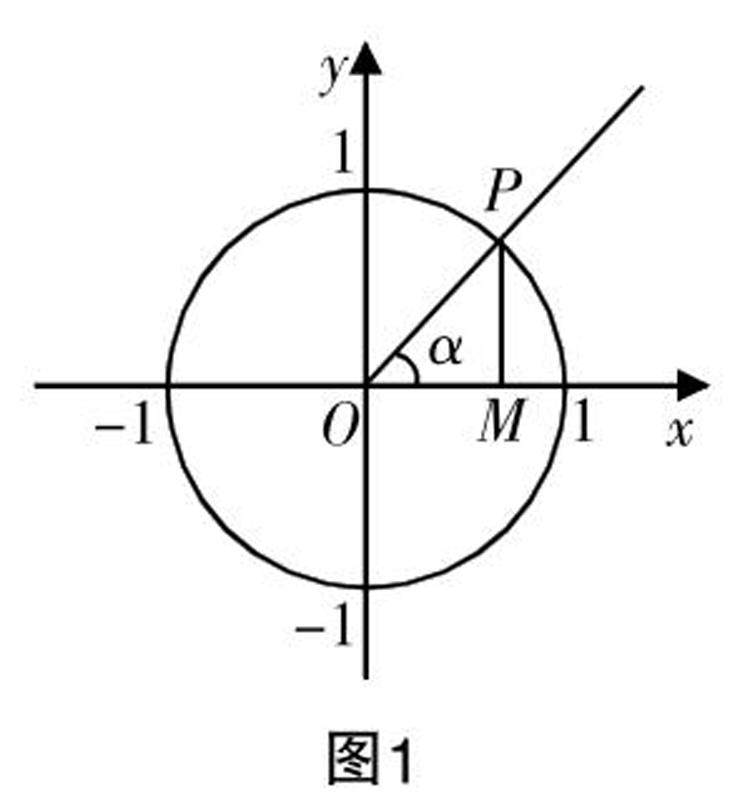
教学实践 | 立足“三个理解”发展核心素养
教学实践 | 立足“三个理解”发展核心素养
-

教学实践 | 以“学”为中心的探究式教学的探索与研究
教学实践 | 以“学”为中心的探究式教学的探索与研究
-

教学实践 | 核心素养导向下指向学力发展的教学路径探索
教学实践 | 核心素养导向下指向学力发展的教学路径探索
-

教学实践 | 放手探究 优化思维 提升素养
教学实践 | 放手探究 优化思维 提升素养
-

问题探索 | 关于立体几何中探究点的位置的教学指导
问题探索 | 关于立体几何中探究点的位置的教学指导
-

问题探索 | HPM视角下“复数”同课异构的实践与思考
问题探索 | HPM视角下“复数”同课异构的实践与思考
-

教学反思 | 数学问题链教学的预设与生成
教学反思 | 数学问题链教学的预设与生成
-

试题研究 | 动静相宜,以“形”见“型”
试题研究 | 动静相宜,以“形”见“型”
-

试题研究 | 关于导数与不等式中的同构探究
试题研究 | 关于导数与不等式中的同构探究
-

试题研究 | 斜率之积(和)为定值时定点、定向问题的求解及推广
试题研究 | 斜率之积(和)为定值时定点、定向问题的求解及推广























 登录
登录