目录
快速导航-
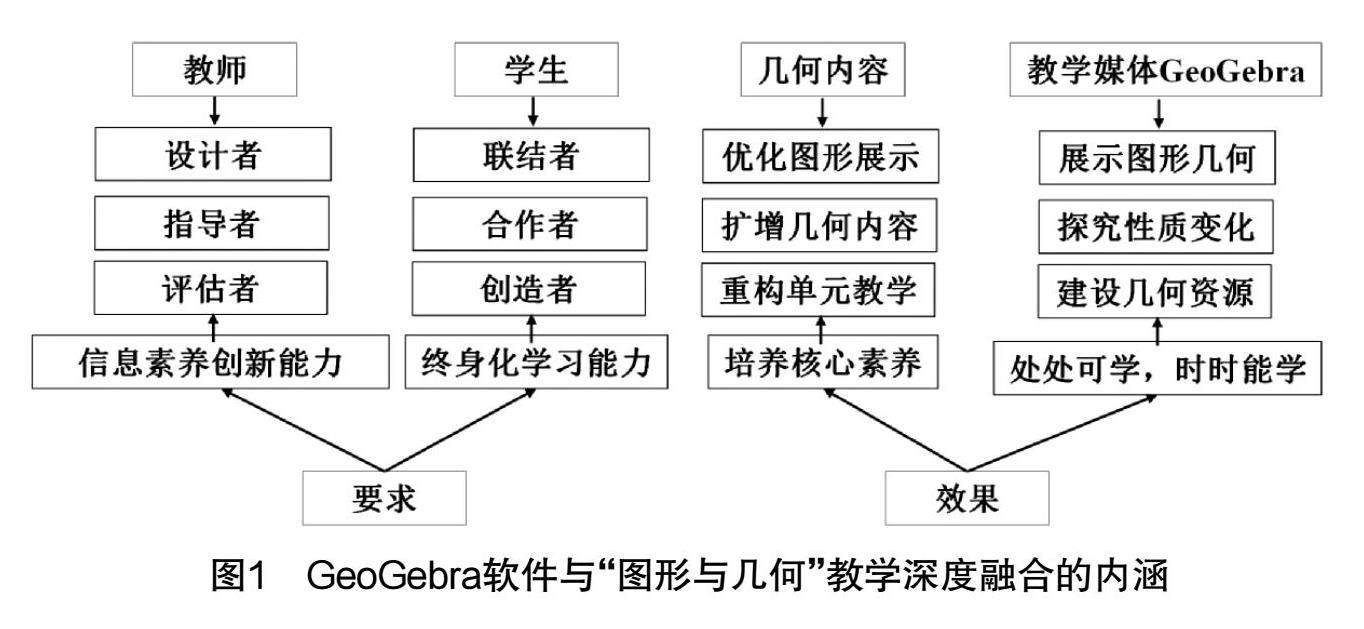
课程教材教法 | 论GeoGebra软件与初中“图形与几何”教学的深度融合
课程教材教法 | 论GeoGebra软件与初中“图形与几何”教学的深度融合
-

课程教材教法 | 研单元整体教学,促核心素养发展
课程教材教法 | 研单元整体教学,促核心素养发展
-
课程教材教法 | 构建整体教学 致力思维生长
课程教材教法 | 构建整体教学 致力思维生长
-

课例分析 | 核心问题引领 提升核心素养
课例分析 | 核心问题引领 提升核心素养
-

课例分析 | 构建生态课堂 回归数学本质
课例分析 | 构建生态课堂 回归数学本质
-

教学实践 | 基于“自主建构”的数学教学研究
教学实践 | 基于“自主建构”的数学教学研究
-
教学实践 | 基于深度学习的课堂教学路径研究
教学实践 | 基于深度学习的课堂教学路径研究
-

教学实践 | 在探究中思考 在思考中提升
教学实践 | 在探究中思考 在思考中提升
-
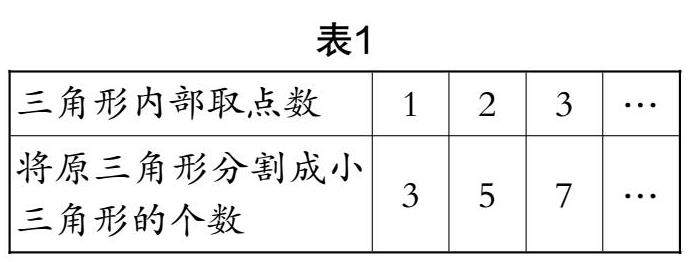
教学实践 | “问题”引领下数学综合实践教学的具体措施
教学实践 | “问题”引领下数学综合实践教学的具体措施
-

教学实践 | 基于合情推理能力发展的问题串设计研究
教学实践 | 基于合情推理能力发展的问题串设计研究
-
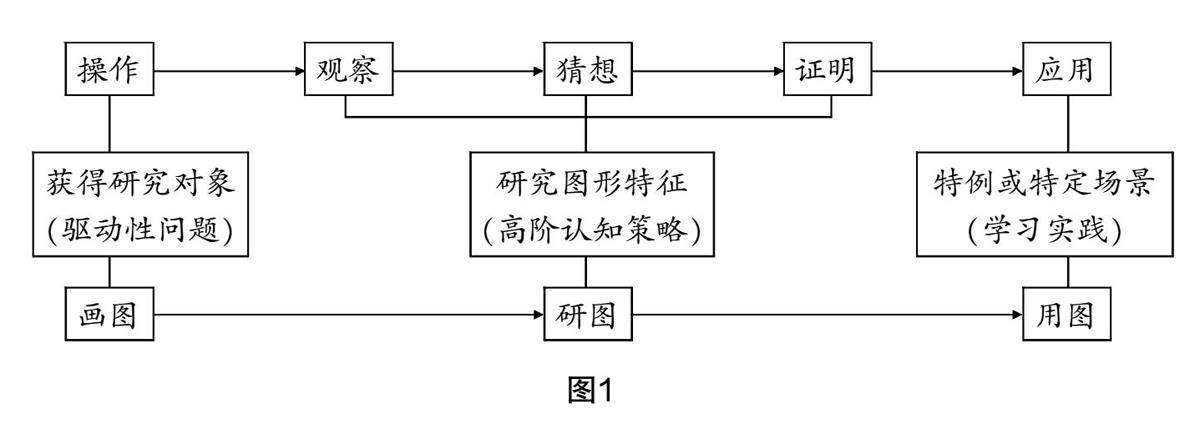
教学实践 | 问题驱动视域下关于初中数学深度教学的探索与思考
教学实践 | 问题驱动视域下关于初中数学深度教学的探索与思考
-

教学实践 | 变构学习模型在初中数学教学中的应用研究
教学实践 | 变构学习模型在初中数学教学中的应用研究
-

教学实践 | 大概念引领 整体化建构
教学实践 | 大概念引领 整体化建构
-

教研在线 | 基于项目式学习的初中数学综合与实践课程的实践研究
教研在线 | 基于项目式学习的初中数学综合与实践课程的实践研究
-
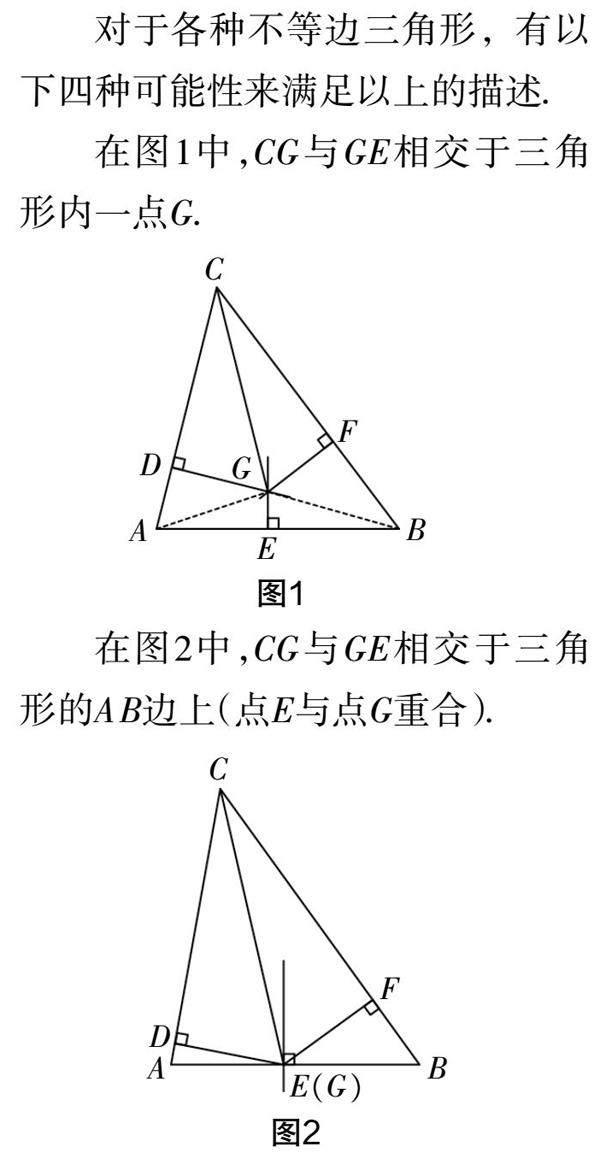
教研在线 | 探命题之伪,促反思之意
教研在线 | 探命题之伪,促反思之意
-
教研在线 | 基于课堂诊断的初中数学教学中“问题”价值的研究
教研在线 | 基于课堂诊断的初中数学教学中“问题”价值的研究
-
教研在线 | 核心素养导向下的初中数学教学设计
教研在线 | 核心素养导向下的初中数学教学设计
-
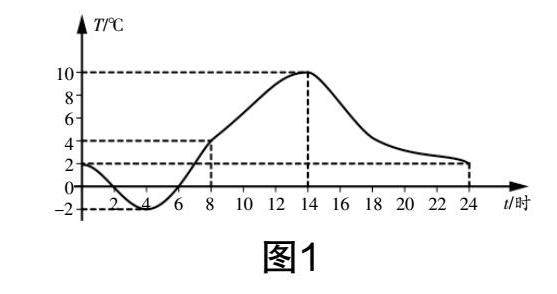
教研在线 | 基于“慢学习”理念的初中数学教学研究
教研在线 | 基于“慢学习”理念的初中数学教学研究
-
教研在线 | 初中数学“本质性教学”策略探寻
教研在线 | 初中数学“本质性教学”策略探寻
-

教研在线 | 初中数学实验类型及其教学范式
教研在线 | 初中数学实验类型及其教学范式
-

教研在线 | “自学·议论·引导”教学法的板书实践研究
教研在线 | “自学·议论·引导”教学法的板书实践研究
-
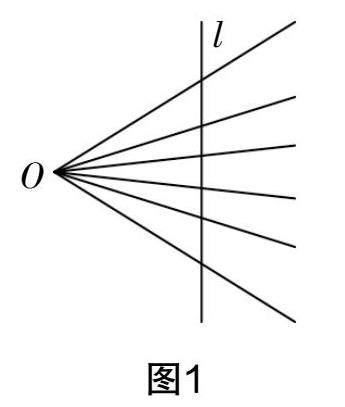
问题探索 | 经历数学抽象过程 提升数学建模素养
问题探索 | 经历数学抽象过程 提升数学建模素养
-

问题探索 | 基于创新思维培养的课堂教学环境营造措施研究
问题探索 | 基于创新思维培养的课堂教学环境营造措施研究
-

问题探索 | 关注建模内涵 划分建模水平培养建模能力
问题探索 | 关注建模内涵 划分建模水平培养建模能力
-

教学技巧 | 开展课堂探究活动 优化初中数学教学
教学技巧 | 开展课堂探究活动 优化初中数学教学
-

教学技巧 | 开展合作探究,提升数学能力
教学技巧 | 开展合作探究,提升数学能力
-

教学技巧 | 拓展例题资源 优化思维品质
教学技巧 | 拓展例题资源 优化思维品质
-
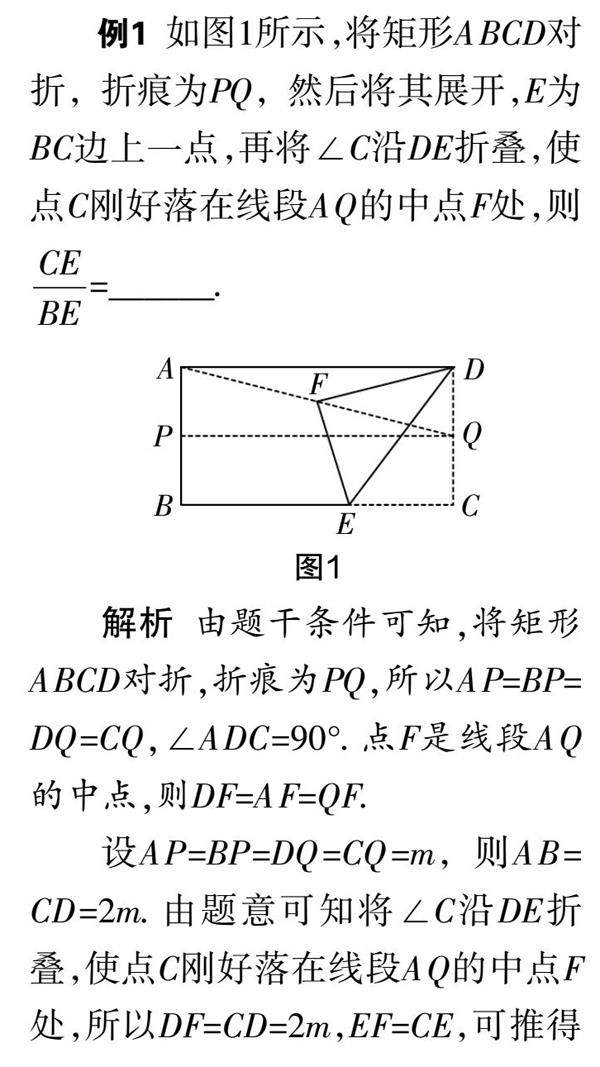
试题探究 | 关于图形变换中的折叠探究
试题探究 | 关于图形变换中的折叠探究
-

试题探究 | 关于二次函数综合题的过程突破与解法探究
试题探究 | 关于二次函数综合题的过程突破与解法探究























 登录
登录