目录
快速导航-
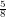
卷首语 | 教师需要怎样的教学主张
卷首语 | 教师需要怎样的教学主张
-

专题研究 | 跨越学段界限的“相对性眼光
专题研究 | 跨越学段界限的“相对性眼光
-

本期话题 | 数学建模在小学数学中的理论探析与价值体现
本期话题 | 数学建模在小学数学中的理论探析与价值体现
-

本期话题 | 数学建模在香港小学数学课程中的隐性体现
本期话题 | 数学建模在香港小学数学课程中的隐性体现
-

本期话题 | 模型意识培养的实践与探索
本期话题 | 模型意识培养的实践与探索
-

本期话题 | “数量关系”建模 作业设计微思
本期话题 | “数量关系”建模 作业设计微思
-

本期话题 | 培养学生数学建模能力:“曹冲称象的故事”教学设计
本期话题 | 培养学生数学建模能力:“曹冲称象的故事”教学设计
-

备课之窗 | 借助直观图式理解数与数的关系
备课之窗 | 借助直观图式理解数与数的关系
-

备课之窗 | 如何借助“分小棒”促进学生对除法竖式含义的理解
备课之窗 | 如何借助“分小棒”促进学生对除法竖式含义的理解
-

备课之窗 | 如何运用“对比”来辨析面积概念
备课之窗 | 如何运用“对比”来辨析面积概念
-

备课之窗 | 如何在小数乘、除法运算中培养推理意识
备课之窗 | 如何在小数乘、除法运算中培养推理意识
-

备课之窗 | 如何帮助学生更好地理解乘法分配律
备课之窗 | 如何帮助学生更好地理解乘法分配律
-

观点主张 | 学生能独立举出例子吗?
观点主张 | 学生能独立举出例子吗?
-

课堂新探 | 基于学习主题的小学数学单元学习路径
课堂新探 | 基于学习主题的小学数学单元学习路径
-

课堂新探 | 探索儿何思维发展的新路径
课堂新探 | 探索儿何思维发展的新路径
-

课堂新探 | 小学数学“微”概念图的价值意蕴与教学策略
课堂新探 | 小学数学“微”概念图的价值意蕴与教学策略
-

课堂新探 | 数形"共生 助行“推理
课堂新探 | 数形"共生 助行“推理
-

特别关注 | 基于学习路径分析的“面积”单元整体教学
特别关注 | 基于学习路径分析的“面积”单元整体教学
-

评价研究 | 素养导向下的小学数学作业设计应把握的五个关键点
评价研究 | 素养导向下的小学数学作业设计应把握的五个关键点
















 登录
登录