目录
快速导航-

课程教材教法 | HPM视角下构建符合学生认知规律的概念教学
课程教材教法 | HPM视角下构建符合学生认知规律的概念教学
-
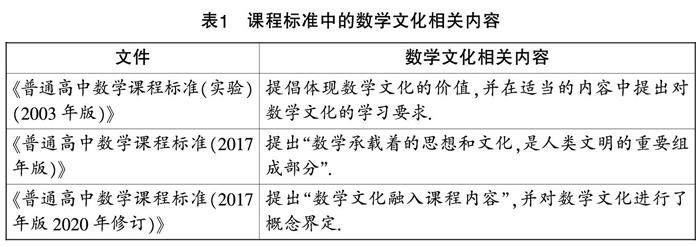
课程教材教法 | 数学文化与高中数学教学研究综述
课程教材教法 | 数学文化与高中数学教学研究综述
-

课程教材教法 | 高中数学教科书旁白的价值及教学策略
课程教材教法 | 高中数学教科书旁白的价值及教学策略
-
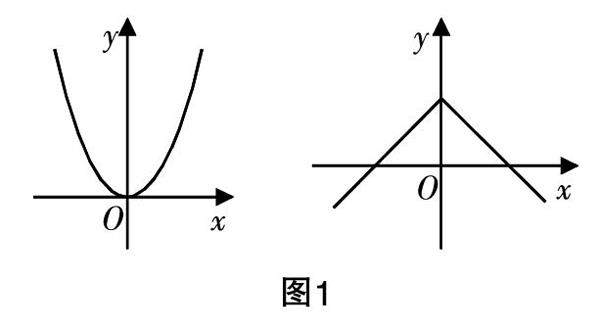
教学实践 | 注重“同课异构”分析,促进概念自然生成
教学实践 | 注重“同课异构”分析,促进概念自然生成
-

教学实践 | 加强变式训练 实现融会贯通
教学实践 | 加强变式训练 实现融会贯通
-

教学实践 | 巧妙设计问题 培养数学素养
教学实践 | 巧妙设计问题 培养数学素养
-

教学实践 | 经历概念形成过程 提升数学抽象素养
教学实践 | 经历概念形成过程 提升数学抽象素养
-

教学实践 | 聚焦深度学习 发展核心素养
教学实践 | 聚焦深度学习 发展核心素养
-

教学实践 | 新高考背景下高中数学概念探究教学有效性研究
教学实践 | 新高考背景下高中数学概念探究教学有效性研究
-

教学实践 | 基于弗赖登塔尔教育思想的“双曲线定义”教学探究
教学实践 | 基于弗赖登塔尔教育思想的“双曲线定义”教学探究
-

教学实践 | 巧用学生的疑惑,促进课堂动态生成
教学实践 | 巧用学生的疑惑,促进课堂动态生成
-

教学实践 | 基于“直观想象素养”发展的数学教学实践与研究
教学实践 | 基于“直观想象素养”发展的数学教学实践与研究
-

教学实践 | 由“函数奇偶性”的概念教学引发的思考
教学实践 | 由“函数奇偶性”的概念教学引发的思考
-

教研在线 | 基于高中生数学学习力增进的任务块教学实践研究
教研在线 | 基于高中生数学学习力增进的任务块教学实践研究
-

教研在线 | 信息技术2.0背景下高中数学课程整合模式研究
教研在线 | 信息技术2.0背景下高中数学课程整合模式研究
-
教研在线 | 深度学习背景下高中数学大单元教学设计研究
教研在线 | 深度学习背景下高中数学大单元教学设计研究
-

教研在线 | 重塑新思维,人工智能助力数学教学
教研在线 | 重塑新思维,人工智能助力数学教学
-

问题探索 | 探究性教学模式在数学教学中的实施
问题探索 | 探究性教学模式在数学教学中的实施
-

问题探索 | 浅析如何在解题教学中发展学生的数学学科核心素养
问题探索 | 浅析如何在解题教学中发展学生的数学学科核心素养
-

问题探索 | 基于抽象素养培养的数学教学研究
问题探索 | 基于抽象素养培养的数学教学研究
-

问题探索 | 数学逻辑思维的作用与培养措施的研究
问题探索 | 数学逻辑思维的作用与培养措施的研究
-

问题探索 | 举反例在数学教学中的应用研究
问题探索 | 举反例在数学教学中的应用研究
-

问题探索 | 自主学习能力培养的必要性与措施的研究
问题探索 | 自主学习能力培养的必要性与措施的研究
-

问题探索 | 基于数据分析素养,引导学生数据探究
问题探索 | 基于数据分析素养,引导学生数据探究
-

教学反思 | 例谈数形结合思想方法在数学教学中的应用与思考
教学反思 | 例谈数形结合思想方法在数学教学中的应用与思考
-

教学反思 | 对二轮复习中“知识专题”复习教学的几点认识
教学反思 | 对二轮复习中“知识专题”复习教学的几点认识
-

教学反思 | 关注教学细节 优化数学教学
教学反思 | 关注教学细节 优化数学教学
-

教学技巧 | 借助创新训练 提升创新能力
教学技巧 | 借助创新训练 提升创新能力
-

试题研究 | 解析几何中非对称式化归的探究与思考
试题研究 | 解析几何中非对称式化归的探究与思考
-

试题研究 | 一道三角形面积最值问题的探究与思考
试题研究 | 一道三角形面积最值问题的探究与思考





















 登录
登录