目录
快速导航-
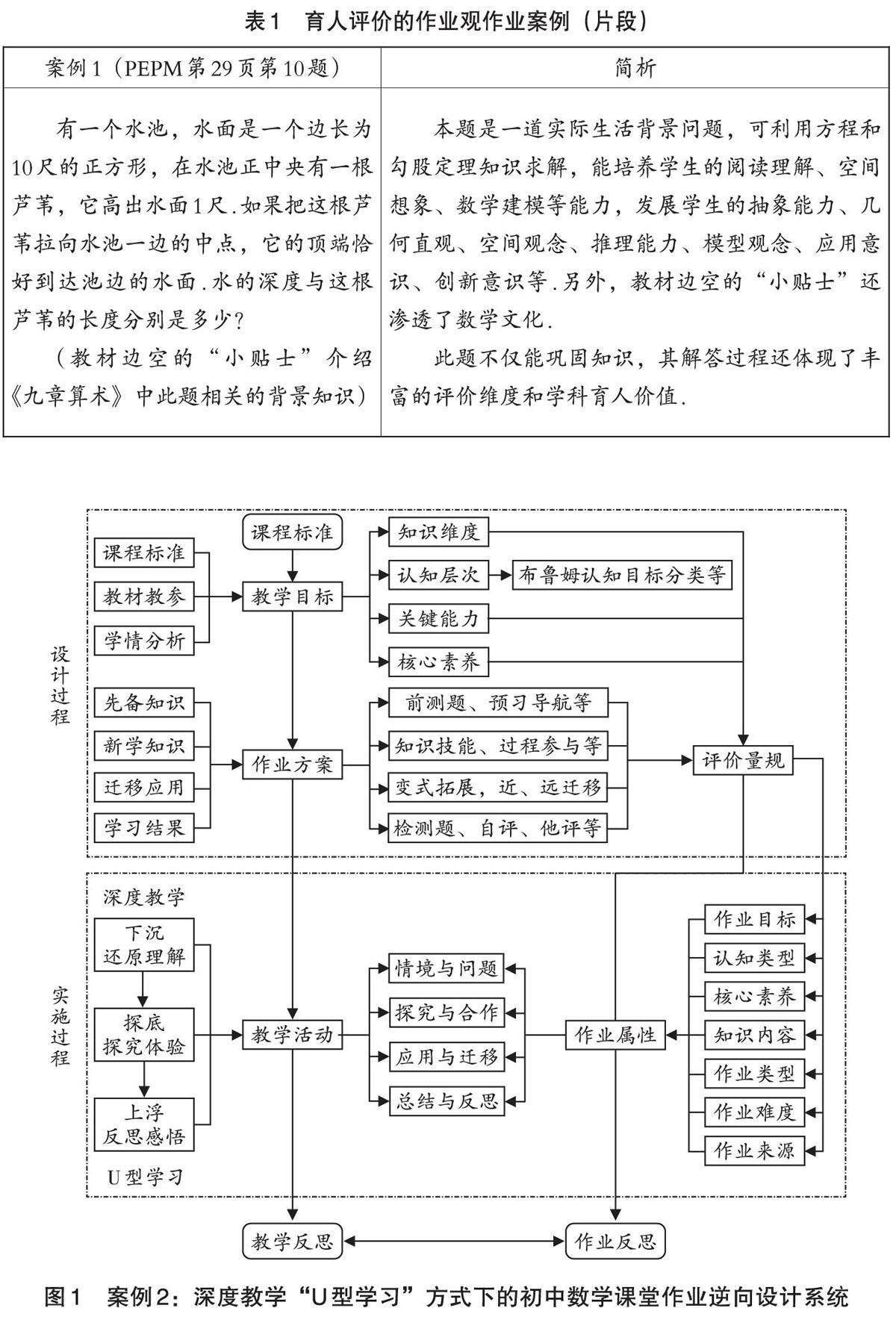
课程教材教法 | 新课程下的初中数学课堂作业优化设计
课程教材教法 | 新课程下的初中数学课堂作业优化设计
-

课程教材教法 | 走进课堂,关注教学一致性研究
课程教材教法 | 走进课堂,关注教学一致性研究
-
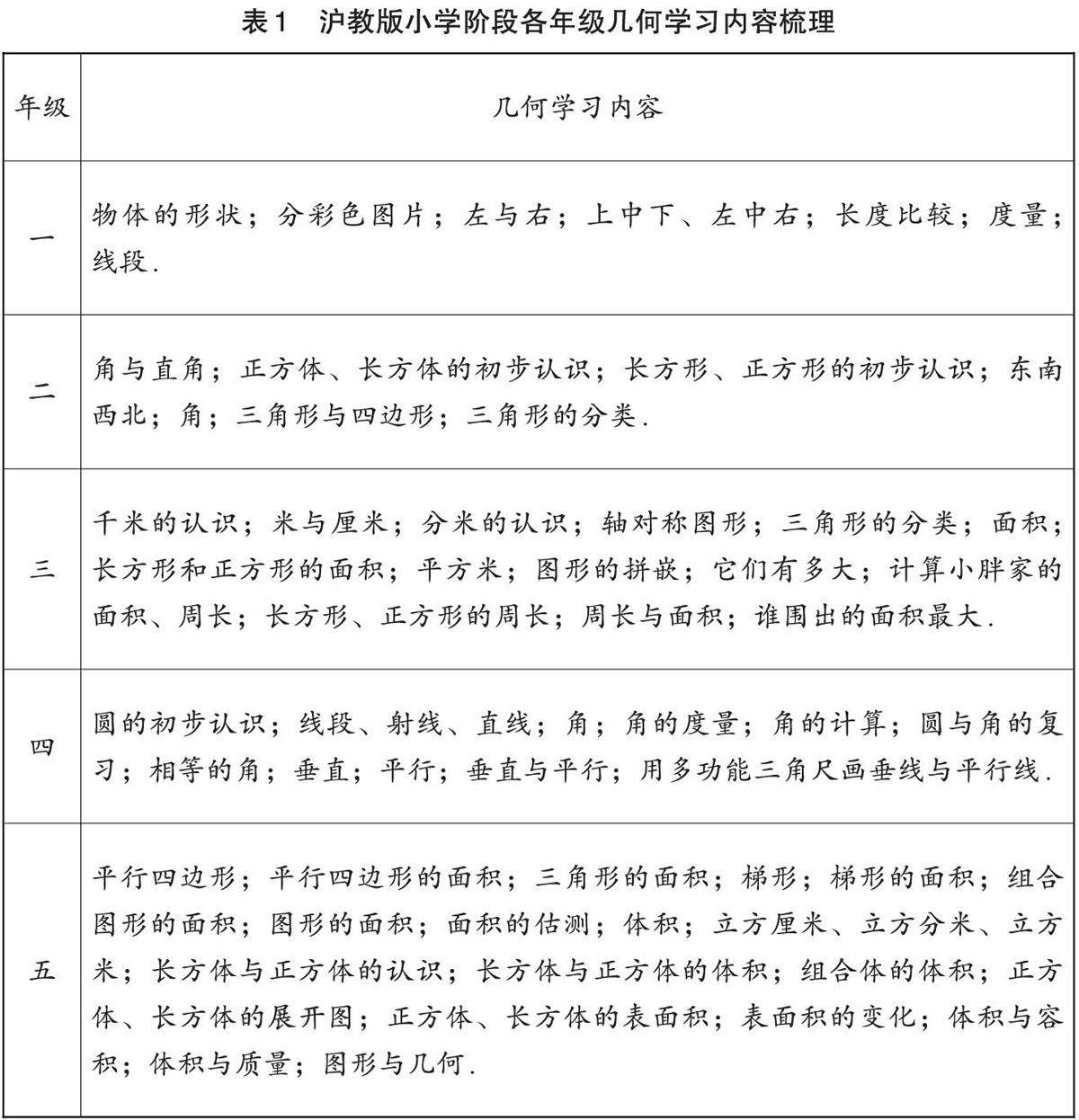
课程教材教法 | 找准起点 渗透思想 点燃思维
课程教材教法 | 找准起点 渗透思想 点燃思维
-

课程教材教法 | 从发展抽象能力的视角研究函数图象的性质
课程教材教法 | 从发展抽象能力的视角研究函数图象的性质
-

课例评析 | 大单元观下的课时实施
课例评析 | 大单元观下的课时实施
-

课例评析 | 渐进“再发现”:在数学活动中悟思想提素养
课例评析 | 渐进“再发现”:在数学活动中悟思想提素养
-
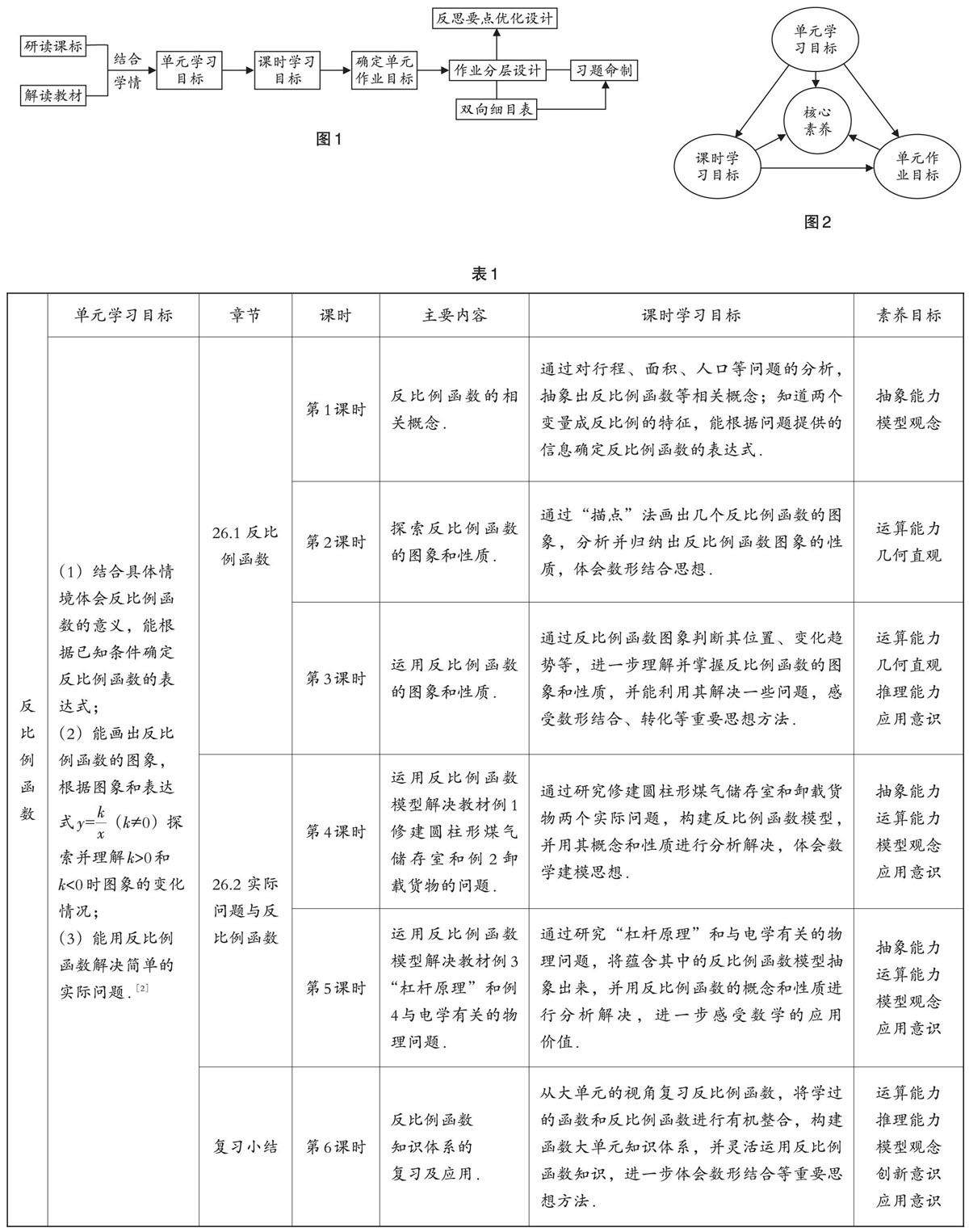
教学实践 | 指向核心素养的初中数学单元作业设计实践
教学实践 | 指向核心素养的初中数学单元作业设计实践
-

教学实践 | “链+”视角下的专题复习生长课堂
教学实践 | “链+”视角下的专题复习生长课堂
-

教学实践 | 基于数学核心素养的大单元教学探索
教学实践 | 基于数学核心素养的大单元教学探索
-

教学实践 | 核心素养背景下基于“生本”理念的教学实践与思考
教学实践 | 核心素养背景下基于“生本”理念的教学实践与思考
-

教学实践 | HPM视域下的初中数学教学研究
教学实践 | HPM视域下的初中数学教学研究
-

教学实践 | 深度学习视角下的数学概念教学策略研究
教学实践 | 深度学习视角下的数学概念教学策略研究
-

教学实践 | 数学概念教学要引领学生走探究之路
教学实践 | 数学概念教学要引领学生走探究之路
-
教研在线 | 深度教学视域下初中数学单元教学设计研究
教研在线 | 深度教学视域下初中数学单元教学设计研究
-
教研在线 | 探究通往学生积极心理的初中数学教学途径
教研在线 | 探究通往学生积极心理的初中数学教学途径
-
教研在线 | 基于“希沃”系统的数学高效课堂教学策略研究
教研在线 | 基于“希沃”系统的数学高效课堂教学策略研究
-
教研在线 | 浅谈核心素养视角下初中数学教材的重构
教研在线 | 浅谈核心素养视角下初中数学教材的重构
-

问题探索 | 核心素养背景下“发现与提出问题”驱动教学的探索
问题探索 | 核心素养背景下“发现与提出问题”驱动教学的探索
-

问题探索 | 实施“有效教学”,让初中数学教学真正“有效”
问题探索 | 实施“有效教学”,让初中数学教学真正“有效”
-
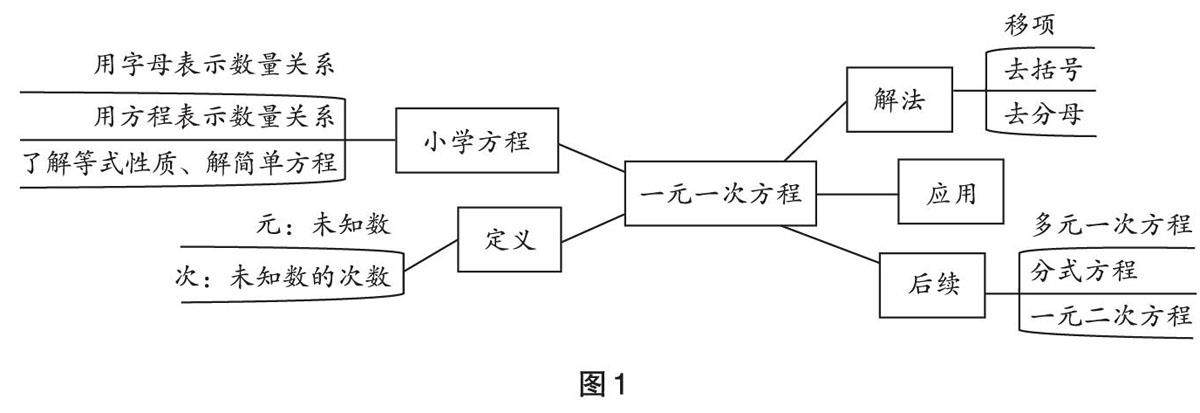
问题探索 | 借助信息技术手段发展数学运算能力的措施研究
问题探索 | 借助信息技术手段发展数学运算能力的措施研究
-
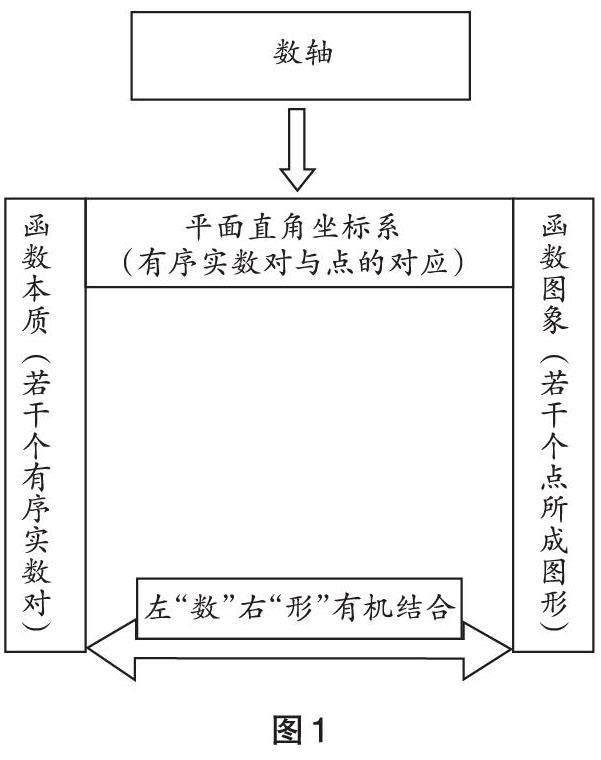
教学反思 | 循序渐进的教学方式是提升数学思维的有效路径
教学反思 | 循序渐进的教学方式是提升数学思维的有效路径
-
教学反思 | 探索教学“慢”艺术,促进课堂更高效
教学反思 | 探索教学“慢”艺术,促进课堂更高效
-
教学技巧 | 开展有效合作 提升课堂实效
教学技巧 | 开展有效合作 提升课堂实效
-
教学技巧 | 让学:初中数学“立学课堂”建构策略
教学技巧 | 让学:初中数学“立学课堂”建构策略
-

试题研究 | 追本溯源扬文化,拓形变式探通法
试题研究 | 追本溯源扬文化,拓形变式探通法
-

试题研究 | 关于等腰三角形构造技巧的探究
试题研究 | 关于等腰三角形构造技巧的探究
-

试题研究 | 问题探究总结方法,定理转化思路构建
试题研究 | 问题探究总结方法,定理转化思路构建
-

试题研究 | 探究解读模型,应用分析探讨
试题研究 | 探究解读模型,应用分析探讨























 登录
登录