目录
快速导航-
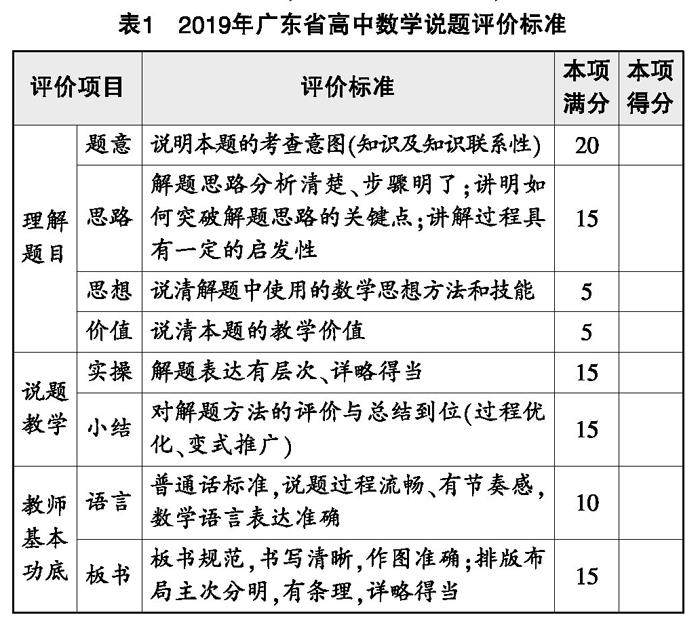
课程教材教法 | 比赛场域下的中学数学教师说题内涵及策略
课程教材教法 | 比赛场域下的中学数学教师说题内涵及策略
-

课程教材教法 | 落实“四翼”考查要求助力创新人才选拔
课程教材教法 | 落实“四翼”考查要求助力创新人才选拔
-

课程教材教法 | 中学数学标准差的理解与教学重构
课程教材教法 | 中学数学标准差的理解与教学重构
-

课程教材教法 | 基于STEM的高中数学建模素养培育框架研究
课程教材教法 | 基于STEM的高中数学建模素养培育框架研究
-
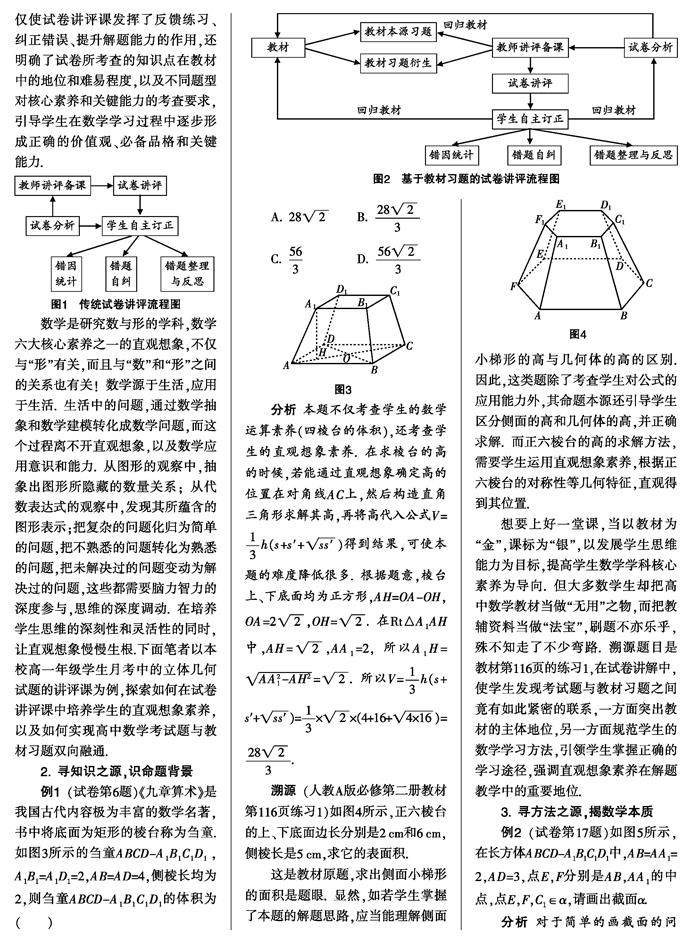
课程教材教法 | 高中数学考试题与教材习题双向融通的实践与思考
课程教材教法 | 高中数学考试题与教材习题双向融通的实践与思考
-

课例评析 | 基于GeoGebra运用的数学教学设计
课例评析 | 基于GeoGebra运用的数学教学设计
-

课例评析 | 聚焦问题驱动发展数学素养
课例评析 | 聚焦问题驱动发展数学素养
-

课例评析 | 抓住概念本质促进深度学习
课例评析 | 抓住概念本质促进深度学习
-

课例评析 | 浅谈新高考背景下“以生为主”的复习课堂构建
课例评析 | 浅谈新高考背景下“以生为主”的复习课堂构建
-
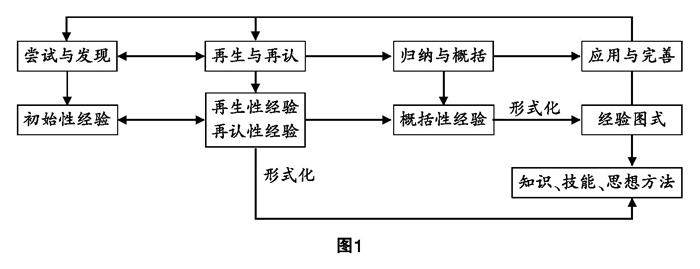
教学实践 | 关注知识建构过程积累数学活动经验
教学实践 | 关注知识建构过程积累数学活动经验
-

教学实践 | 基于内容本质的教学路径的探索
教学实践 | 基于内容本质的教学路径的探索
-

教学实践 | 基于整体思考推进章节复习教学
教学实践 | 基于整体思考推进章节复习教学
-

教学实践 | 充分发挥学生主体作用提升单元复习教学品质
教学实践 | 充分发挥学生主体作用提升单元复习教学品质
-

教学实践 | 大数据背景下的数学精准教学研究与感悟
教学实践 | 大数据背景下的数学精准教学研究与感悟
-

教学实践 | 关注知识联系突出融合关系发展核心素养
教学实践 | 关注知识联系突出融合关系发展核心素养
-

教学实践 | 关注微专题复习发展数学核心素养
教学实践 | 关注微专题复习发展数学核心素养
-

教学实践 | 类比引领课堂探究成就精彩
教学实践 | 类比引领课堂探究成就精彩
-

教学实践 | 概念教学中发展数学学科核心素养的实践与研究
教学实践 | 概念教学中发展数学学科核心素养的实践与研究
-

教研在线 | 聚焦“以题塑人”落实“立德树人”
教研在线 | 聚焦“以题塑人”落实“立德树人”
-

教研在线 | “双减”背景下基于大数据支持的中学校本作业设计与实施研究
教研在线 | “双减”背景下基于大数据支持的中学校本作业设计与实施研究
-

教研在线 | 用现象教学促进学生深度学习的实践与研究
教研在线 | 用现象教学促进学生深度学习的实践与研究
-

教研在线 | 从师生两个层面剖析“懂而不会”现象
教研在线 | 从师生两个层面剖析“懂而不会”现象
-

问题探索 | 核心素养背景下求解探究性问题的方法研究
问题探索 | 核心素养背景下求解探究性问题的方法研究
-

问题探索 | 信息技术在高中数学课堂中的应用研究
问题探索 | 信息技术在高中数学课堂中的应用研究
-
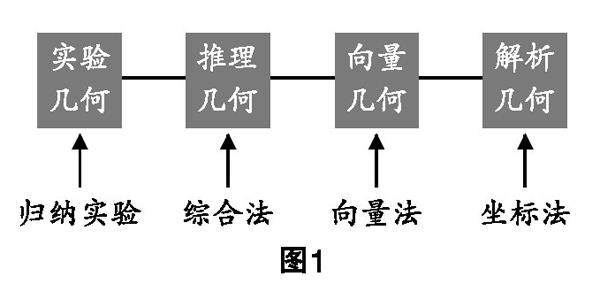
问题探索 | 关于“直线的倾斜角与斜率”的教学探究思考
问题探索 | 关于“直线的倾斜角与斜率”的教学探究思考
-

问题探索 | 对培养学生提出问题能力的思考与实践
问题探索 | 对培养学生提出问题能力的思考与实践
-

教学技巧 | 核心素养下的高中数学概念教学
教学技巧 | 核心素养下的高中数学概念教学
-

教学技巧 | 应用探究:探索发现,论证生成
教学技巧 | 应用探究:探索发现,论证生成
-
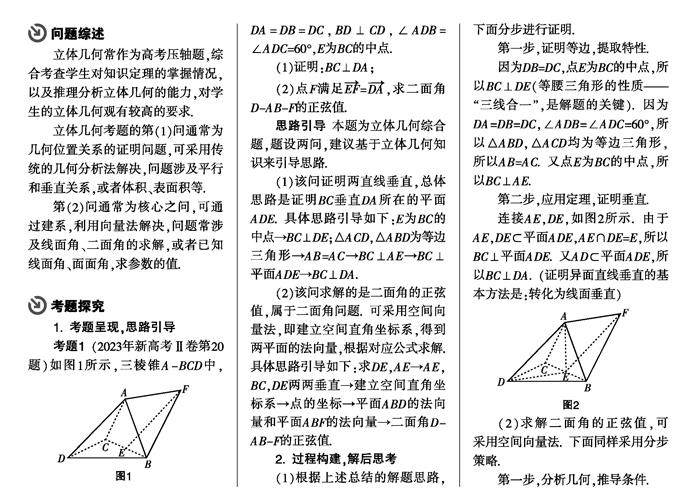
试题研究 | 关于一道立体几何考题的探究总结与教学思考
试题研究 | 关于一道立体几何考题的探究总结与教学思考
-

试题研究 | 多视角探究高考解析几何问题
试题研究 | 多视角探究高考解析几何问题
-

试题研究 | 一道多变元代数式最值模拟试题的解法探究
试题研究 | 一道多变元代数式最值模拟试题的解法探究





















 登录
登录