目录
快速导航-
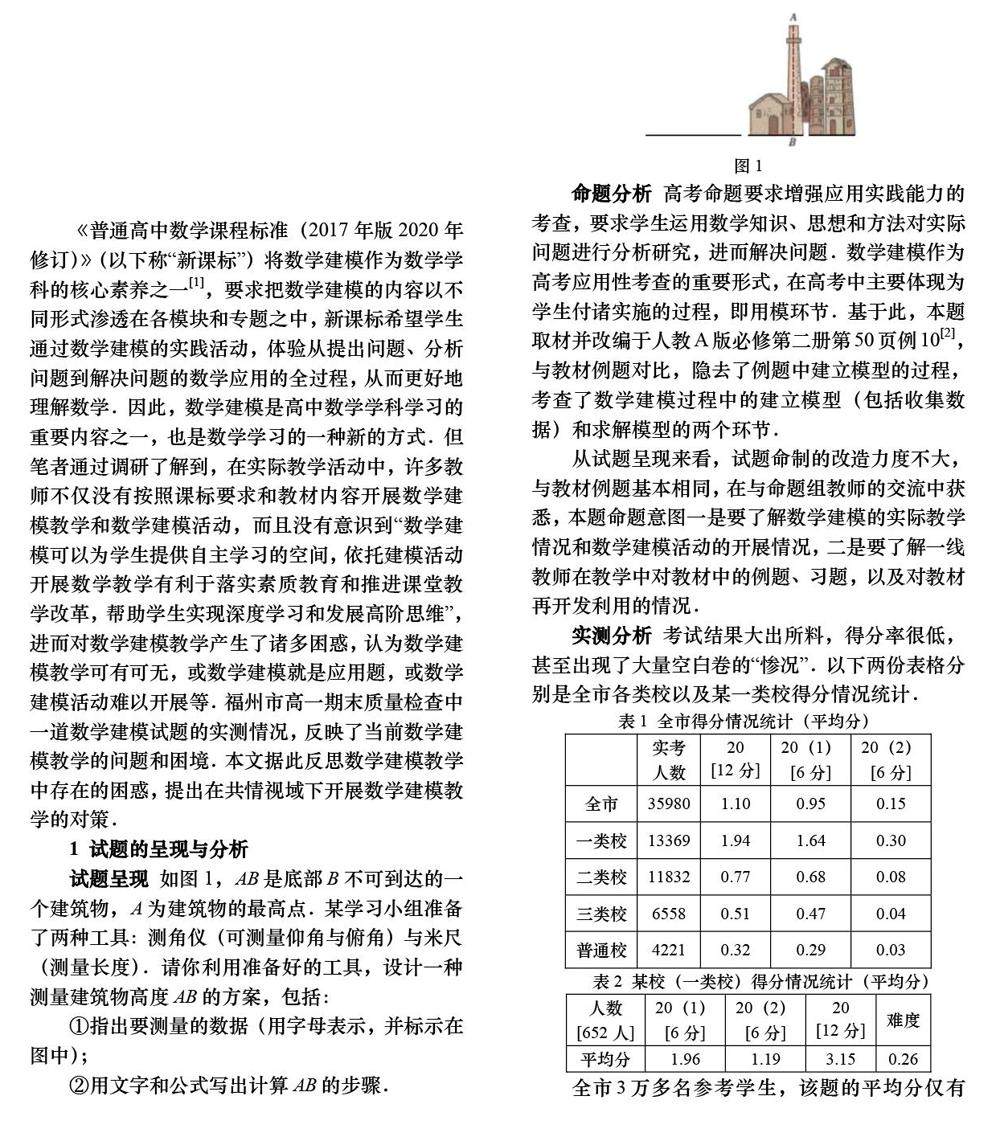
数学教育 | 共情视域下高中数学建模教学的困惑与对策
数学教育 | 共情视域下高中数学建模教学的困惑与对策
-

数学教育 | 落实核心素养 培养初中生数学解题能力
数学教育 | 落实核心素养 培养初中生数学解题能力
-

教学研究 | 分类讨论的教学价值和教学实施
教学研究 | 分类讨论的教学价值和教学实施
-

教学研究 | 数学文化引领下的教学设计
教学研究 | 数学文化引领下的教学设计
-

教学研究 | 指向关键能力提升的数学微专题的教学设计
教学研究 | 指向关键能力提升的数学微专题的教学设计
-

教学研究 | 一般观念指导的单元起始课
教学研究 | 一般观念指导的单元起始课
-

考试研究 | 立足课标 指向素养 弱化模式 回归本质
考试研究 | 立足课标 指向素养 弱化模式 回归本质
-

考试研究 | 基于数学实验的高考数学命题研究与实践
考试研究 | 基于数学实验的高考数学命题研究与实践
-
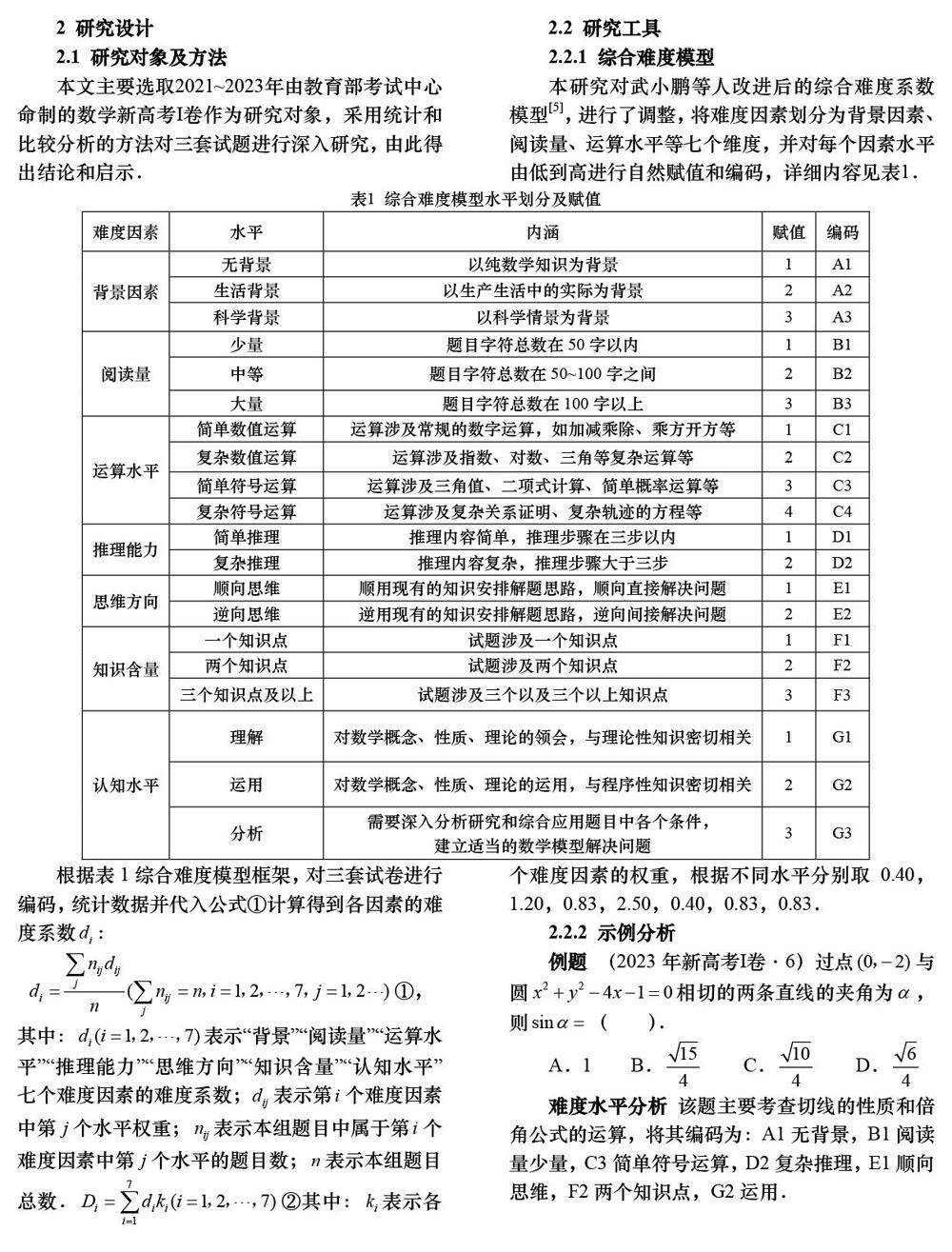
考试研究 | 基于综合难度模型的高考数学试题分析
考试研究 | 基于综合难度模型的高考数学试题分析
-

学习导航 | 从解题到解决问题
学习导航 | 从解题到解决问题
-
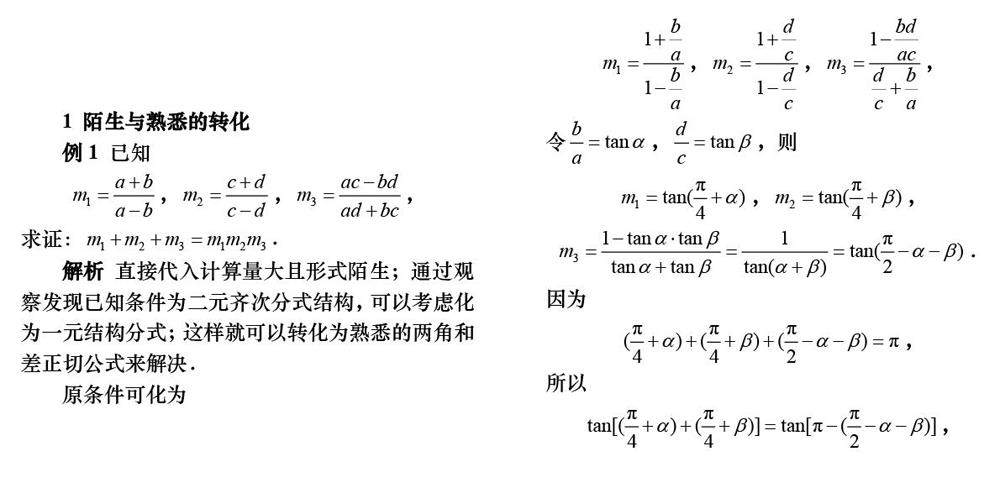
学习导航 | 例谈转化与化归思想的应用
学习导航 | 例谈转化与化归思想的应用
-

学习导航 | 例说比大小问题的常用解题策略
学习导航 | 例说比大小问题的常用解题策略
-

学习导航 | 误中悟:基于直观想象素养的解题策略探究
学习导航 | 误中悟:基于直观想象素养的解题策略探究
-

学习导航 | 咬文嚼字 探究本质
学习导航 | 咬文嚼字 探究本质
-

数学竞赛 | 一道全国高中数学联赛加试题的另解
数学竞赛 | 一道全国高中数学联赛加试题的另解
-

数学竞赛 | 一道全国高中数学联赛预赛试题的多种解法及命题手法
数学竞赛 | 一道全国高中数学联赛预赛试题的多种解法及命题手法























 登录
登录