- 全部分类/
- 中学教育/
- 中学生数理化·高一数学
 扫码免费借阅
扫码免费借阅
目录
快速导航-

知识结构与拓展 | 平面向量及其应用典型题型及解题策略
知识结构与拓展 | 平面向量及其应用典型题型及解题策略
-

知识结构与拓展 | 复数问题学习指导
知识结构与拓展 | 复数问题学习指导
-

知识结构与拓展 | 三角形中的特殊线段及其应用
知识结构与拓展 | 三角形中的特殊线段及其应用
-

知识结构与拓展 | 例说正弦定理与余弦定理的综合应用
知识结构与拓展 | 例说正弦定理与余弦定理的综合应用
-

知识结构与拓展 | 平面向量及其应用学习要点聚焦
知识结构与拓展 | 平面向量及其应用学习要点聚焦
-

知识结构与拓展 | 三角形中的最值与范围问题的求解策略
知识结构与拓展 | 三角形中的最值与范围问题的求解策略
-

知识结构与拓展 | 平面向量数量积的求解策略
知识结构与拓展 | 平面向量数量积的求解策略
-

知识结构与拓展 | 例说与向量有关的最值问题的求解策略
知识结构与拓展 | 例说与向量有关的最值问题的求解策略
-
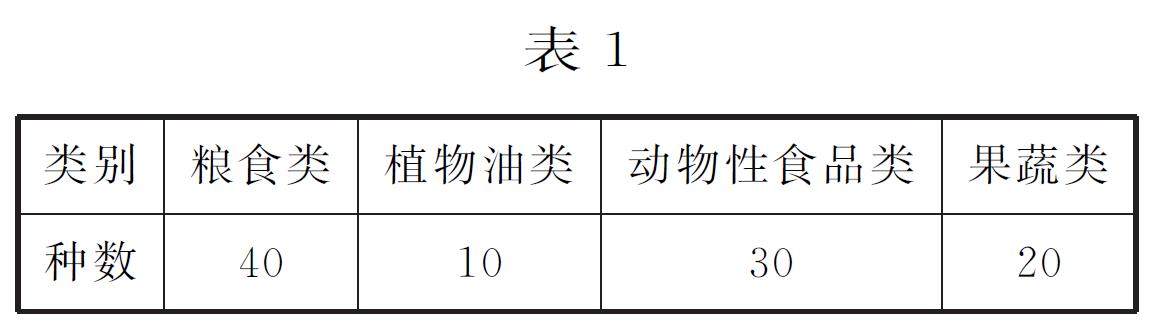
知识结构与拓展 | 例析统计问题中的学习要点
知识结构与拓展 | 例析统计问题中的学习要点
-
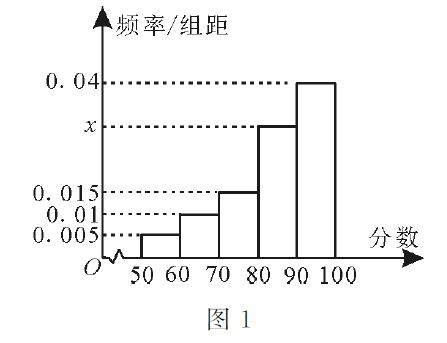
知识结构与拓展 | 基于频率分布直方图的应用视角
知识结构与拓展 | 基于频率分布直方图的应用视角
-

知识结构与拓展 | 巧用复数性质 优化解题过程
知识结构与拓展 | 巧用复数性质 优化解题过程
-

知识结构与拓展 | 五类概率的重难点题型体验
知识结构与拓展 | 五类概率的重难点题型体验
-

核心考点演练 | 高一下学期期末复习综合演练
核心考点演练 | 高一下学期期末复习综合演练
-

创新题追根溯源 | 向量创新问题的求解策略
创新题追根溯源 | 向量创新问题的求解策略
-

创新题追根溯源 | 移、割、折、投
创新题追根溯源 | 移、割、折、投
-

创新题追根溯源 | 复数高考常考题型扫描
创新题追根溯源 | 复数高考常考题型扫描
-

经典题突破方法 | 概率问题常见考点赏析
经典题突破方法 | 概率问题常见考点赏析
-

经典题突破方法 | 玩转古典概型
经典题突破方法 | 玩转古典概型
-

经典题突破方法 | 立体几何初步常见考题聚焦
经典题突破方法 | 立体几何初步常见考题聚焦
-

经典题突破方法 | 复数的压轴题型的“锦囊妙计”
经典题突破方法 | 复数的压轴题型的“锦囊妙计”





















 登录
登录