目录
快速导航-

数学教育 | 上海市初中毕业数学学业考试与课程标准的一致性研究
数学教育 | 上海市初中毕业数学学业考试与课程标准的一致性研究
-
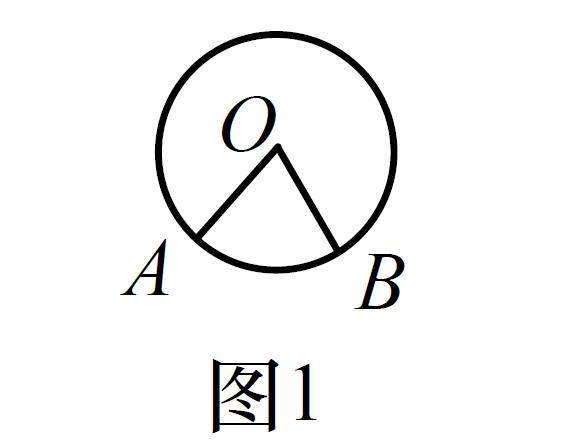
教学研究 | 聚焦一般观念教学 经历定理生成过程
教学研究 | 聚焦一般观念教学 经历定理生成过程
-

教学研究 | 对教材章节章头语及章头图的教学思考
教学研究 | 对教材章节章头语及章头图的教学思考
-

教学研究 | 指向数学高阶思维培养的教学设计
教学研究 | 指向数学高阶思维培养的教学设计
-
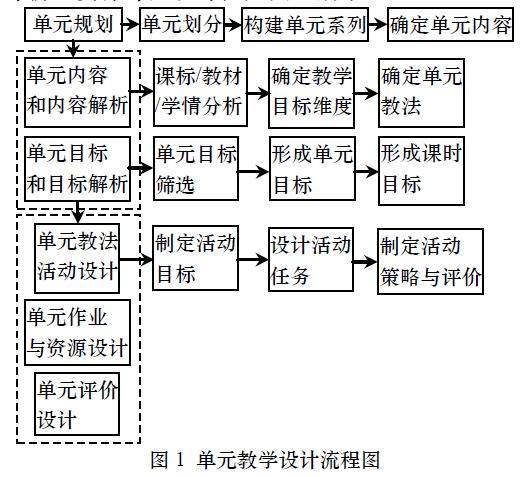
教学研究 | 基于深度学习的高中数学单元教学设计研究
教学研究 | 基于深度学习的高中数学单元教学设计研究
-

教学研究 | 在解题教学中培养数学思维
教学研究 | 在解题教学中培养数学思维
-

教学研究 | 基于“两个过程”合理性思考的生成课堂
教学研究 | 基于“两个过程”合理性思考的生成课堂
-

数学探究 | 一类解析几何极值问题的探究与启示
数学探究 | 一类解析几何极值问题的探究与启示
-

数学探究 | 新教材对数比大小问题的探究与应用
数学探究 | 新教材对数比大小问题的探究与应用
-

考试研究 | 用函数解决实际问题考查抽象能力
考试研究 | 用函数解决实际问题考查抽象能力
-

考试研究 | 一道2022年THUSSAT试题的解法探究
考试研究 | 一道2022年THUSSAT试题的解法探究
-

考试研究 | 一道中学生标准学术能力测试题的解法探究
考试研究 | 一道中学生标准学术能力测试题的解法探究
-

考试研究 | 基于函数对称性的一道试题命制
考试研究 | 基于函数对称性的一道试题命制
-

学习导航 | 化常法破解数列求和
学习导航 | 化常法破解数列求和
-

学习导航 | 例谈“算两次”原理在解三角形中的应用
学习导航 | 例谈“算两次”原理在解三角形中的应用
-

学习导航 | 一道三角形面积最值问题的解法探究及推广
学习导航 | 一道三角形面积最值问题的解法探究及推广
-

数学建模 | 数学建模视角下的情境化问题探究
数学建模 | 数学建模视角下的情境化问题探究























 登录
登录