目录
快速导航-
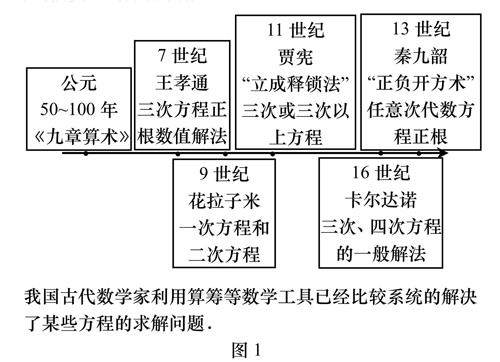
数学教育 | 高中数学“课程思政”的实践与思考
数学教育 | 高中数学“课程思政”的实践与思考
-
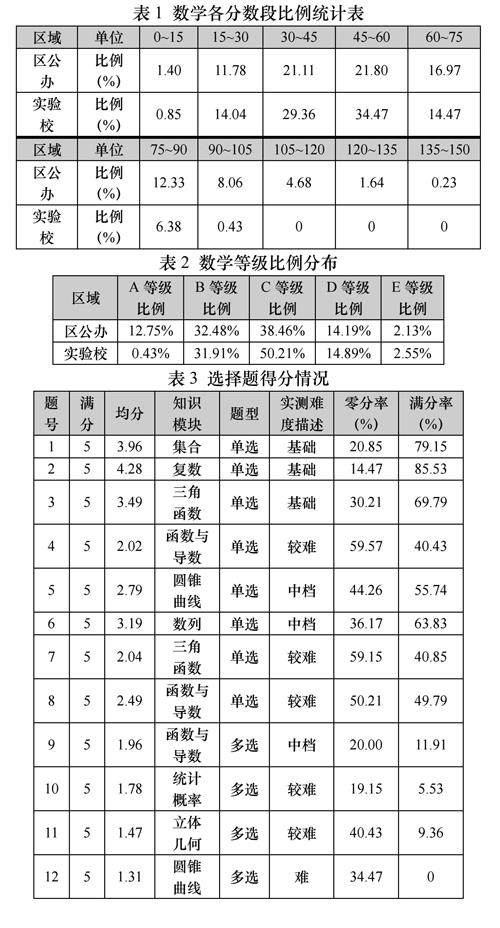
数学教育 | 薄弱高中校数学前置性作业的设计策略
数学教育 | 薄弱高中校数学前置性作业的设计策略
-
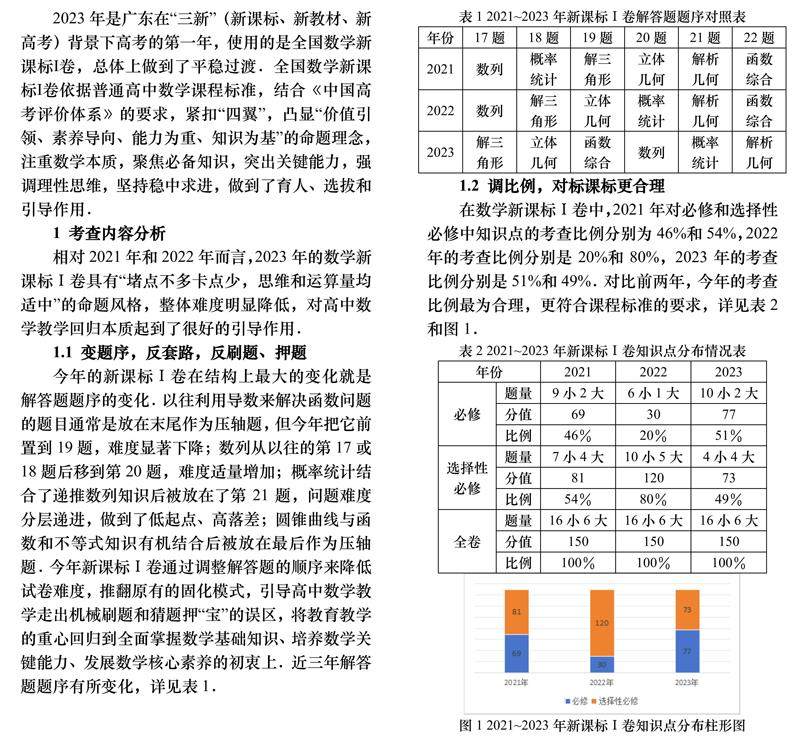
数学教育 | 紧扣“四翼”,助力人才选拔和“双减”落地
数学教育 | 紧扣“四翼”,助力人才选拔和“双减”落地
-
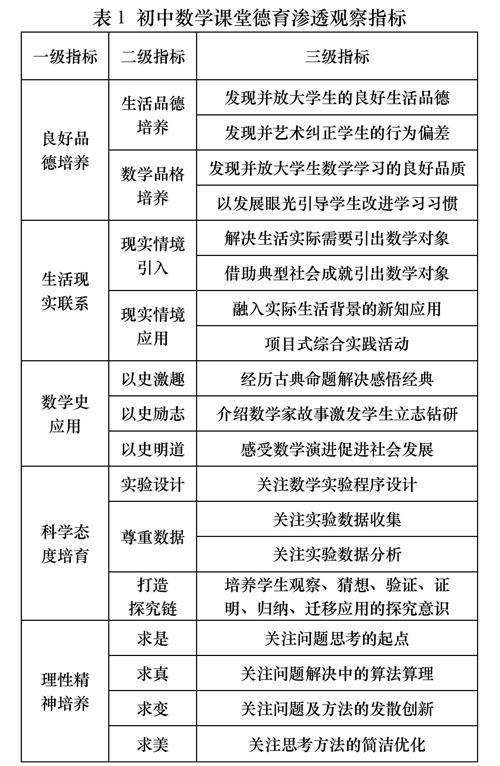
数学教育 | 以精促实:精准聚焦精到落实精恰提升
数学教育 | 以精促实:精准聚焦精到落实精恰提升
-

数学教育 | 注重代数推理发展理性思维
数学教育 | 注重代数推理发展理性思维
-

教学研究 | 提高高中生“数学运算速度”的教学策略
教学研究 | 提高高中生“数学运算速度”的教学策略
-

教学研究 | 用项目学习法建构二次函数动点定值教学研究
教学研究 | 用项目学习法建构二次函数动点定值教学研究
-
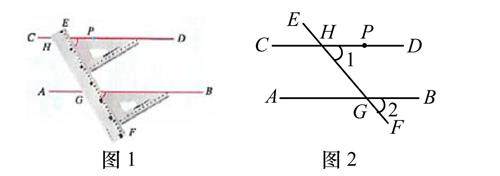
教学研究 | 妙用“问题串”破难点 巧借“情境”提素养
教学研究 | 妙用“问题串”破难点 巧借“情境”提素养
-
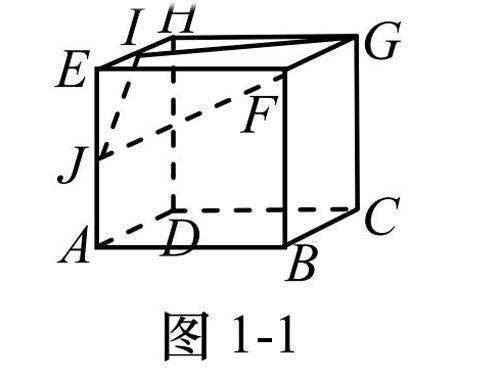
教学研究 | 例谈多面体截面的作法
教学研究 | 例谈多面体截面的作法
-

数学探究 | 探究圆锥曲线中五类存在性问题
数学探究 | 探究圆锥曲线中五类存在性问题
-

考试研究 | 高考数学试题综合难度的比较研究
考试研究 | 高考数学试题综合难度的比较研究
-

考试研究 | 基于非对称韦达定理模型的2023年新高考全国II卷第21题溯源探究与推广
考试研究 | 基于非对称韦达定理模型的2023年新高考全国II卷第21题溯源探究与推广
-

学习导航 | 回归教材一题多变优化思维
学习导航 | 回归教材一题多变优化思维
-

学习导航 | 一道最大视角模考题的思考
学习导航 | 一道最大视角模考题的思考























 登录
登录