目录
快速导航-
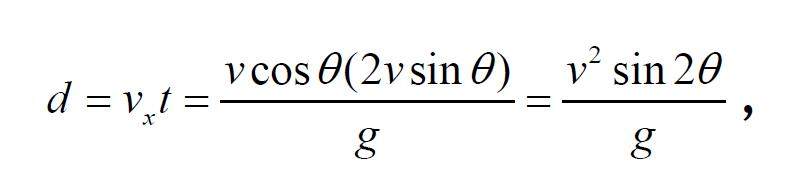
数学教育 | ChatGPT对中学数学建模教育的重构
数学教育 | ChatGPT对中学数学建模教育的重构
-
数学教育 | 如何在高中数学课堂中培养学生的数学表达能力
数学教育 | 如何在高中数学课堂中培养学生的数学表达能力
-

教学研究 | 通过逆向设计 开发数学应用素材 实现教学评一致
教学研究 | 通过逆向设计 开发数学应用素材 实现教学评一致
-

教学研究 | 引发认知冲突实现有效纠错
教学研究 | 引发认知冲突实现有效纠错
-

教学研究 | 和谐视域下“条件概率”教学探索
教学研究 | 和谐视域下“条件概率”教学探索
-

教学研究 | 核心素养下高三数学例题教学探析
教学研究 | 核心素养下高三数学例题教学探析
-
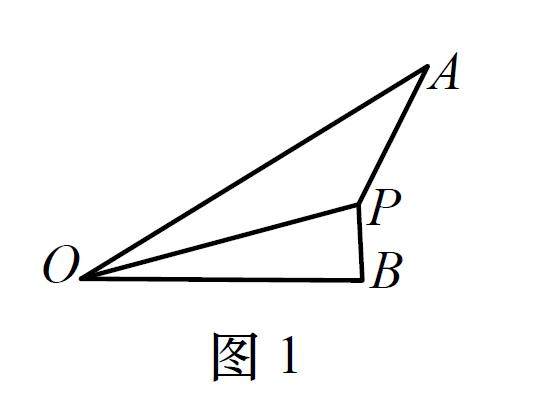
教学研究 | 关联基本图形 培育动态眼光
教学研究 | 关联基本图形 培育动态眼光
-

教学研究 | 基于跨学科学习的初三数学测量方案的探究性学习
教学研究 | 基于跨学科学习的初三数学测量方案的探究性学习
-
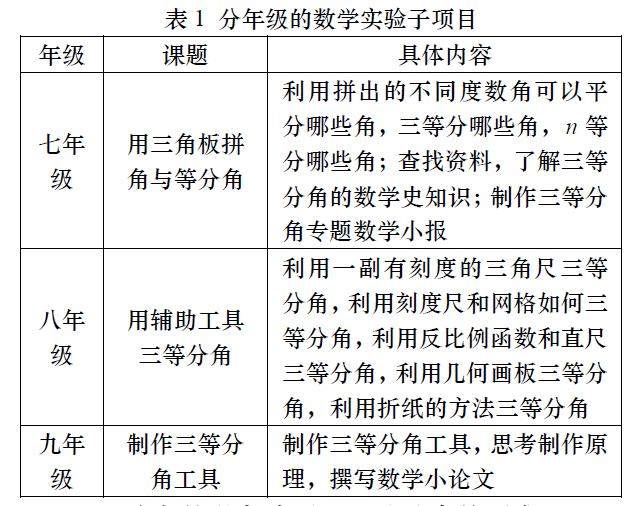
教学研究 | 项目化初中数学实验教学的实践研究
教学研究 | 项目化初中数学实验教学的实践研究
-

数学探究 | 观察与联想在高中数学解题中的应用
数学探究 | 观察与联想在高中数学解题中的应用
-

试题研究 | 追求直观 凸显本质
试题研究 | 追求直观 凸显本质
-

试题研究 | 一道培训班试题的解法赏析及推广
试题研究 | 一道培训班试题的解法赏析及推广
-

试题研究 | 如何裁剪更艺术?
试题研究 | 如何裁剪更艺术?
-

学习导航 | 逆用求导法则 合理构造函数
学习导航 | 逆用求导法则 合理构造函数
-

学习导航 | 三角形有两解条件下边的取值范围问题
学习导航 | 三角形有两解条件下边的取值范围问题
-

学习导航 | 对教材一道抛物线习题的五维深度拓展
学习导航 | 对教材一道抛物线习题的五维深度拓展
-

信息技术 | 利用画板软件 构造奇异曲线
信息技术 | 利用画板软件 构造奇异曲线























 登录
登录