目录
快速导航-
卷首语 | 数学宇宙中的摘星人
卷首语 | 数学宇宙中的摘星人
-
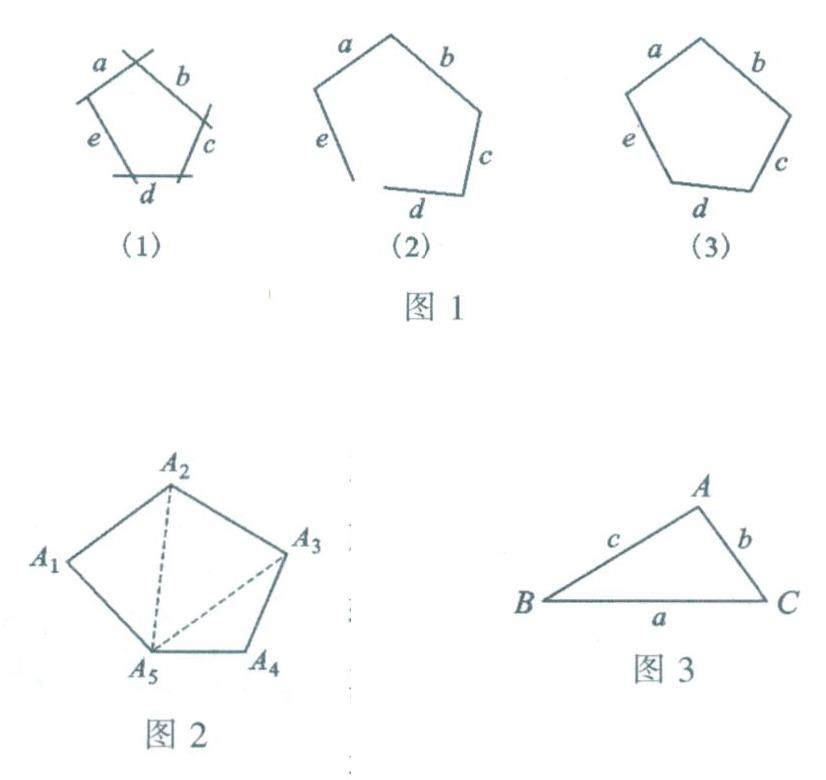
数学之基 | 漫话三角形
数学之基 | 漫话三角形
-

数学之基 | 三边关系了于心 推理辨析明应用
数学之基 | 三边关系了于心 推理辨析明应用
-

数学之基 | 加深概念理解 掌握题型攻略
数学之基 | 加深概念理解 掌握题型攻略
-

数学之基 | 悟数学思想 学解题方法
数学之基 | 悟数学思想 学解题方法
-

数学之基 | “双角平分线”模型的探究与应用
数学之基 | “双角平分线”模型的探究与应用
-

数学之基 | 一道多角求和题的多解与多思
数学之基 | 一道多角求和题的多解与多思
-

数学之基 | 多角少角皆可求
数学之基 | 多角少角皆可求
-

数学之基 | 三角形易错点警示
数学之基 | 三角形易错点警示
-

数学之趣 | 什么问题的答案是42
数学之趣 | 什么问题的答案是42
-

数学之趣 | 当当闯关记
数学之趣 | 当当闯关记
-

数学之趣 | 数学潜能知识竞赛
数学之趣 | 数学潜能知识竞赛
-

数学之用 | “三角形”新题总动员
数学之用 | “三角形”新题总动员
-

数学之用 | “与三角形有关的线段”基础巩固
数学之用 | “与三角形有关的线段”基础巩固
-

数学之用 | “与三角形有关的角”重点检测
数学之用 | “与三角形有关的角”重点检测
-

数学之用 | “多边形及其内角和”要点过关
数学之用 | “多边形及其内角和”要点过关
-

数学之用 | “三角形”易错题专练
数学之用 | “三角形”易错题专练
-

数学之用 | 本期练习类题目参考答案提示
数学之用 | 本期练习类题目参考答案提示






















 登录
登录