目录
快速导航-
卷首语 | 青云之志,赤子之心
卷首语 | 青云之志,赤子之心
-
数学之基 | 平行四边形的定义、性质与判定
数学之基 | 平行四边形的定义、性质与判定
-

数学之基 | 正方形中架“十”字垂直相等总相伴
数学之基 | 正方形中架“十”字垂直相等总相伴
-

数学之基 | 有关矩形的一个重要结论
数学之基 | 有关矩形的一个重要结论
-

数学之基 | 平行四边形与尺规作图的融合
数学之基 | 平行四边形与尺规作图的融合
-

数学之基 | 巧用含60°角的菱形
数学之基 | 巧用含60°角的菱形
-

数学之基 | 斜边中线的妙用
数学之基 | 斜边中线的妙用
-

数学之基 | 酷爱折叠的平行四边形
数学之基 | 酷爱折叠的平行四边形
-

数学之基 | 并肩携手的特殊平行四边形
数学之基 | 并肩携手的特殊平行四边形
-

数学之趣 | 怎样加固一个正方形
数学之趣 | 怎样加固一个正方形
-

数学之趣 | 数学潜能知识竞赛
数学之趣 | 数学潜能知识竞赛
-
数学之趣 | 告别假努力,奋斗正当时
数学之趣 | 告别假努力,奋斗正当时
-
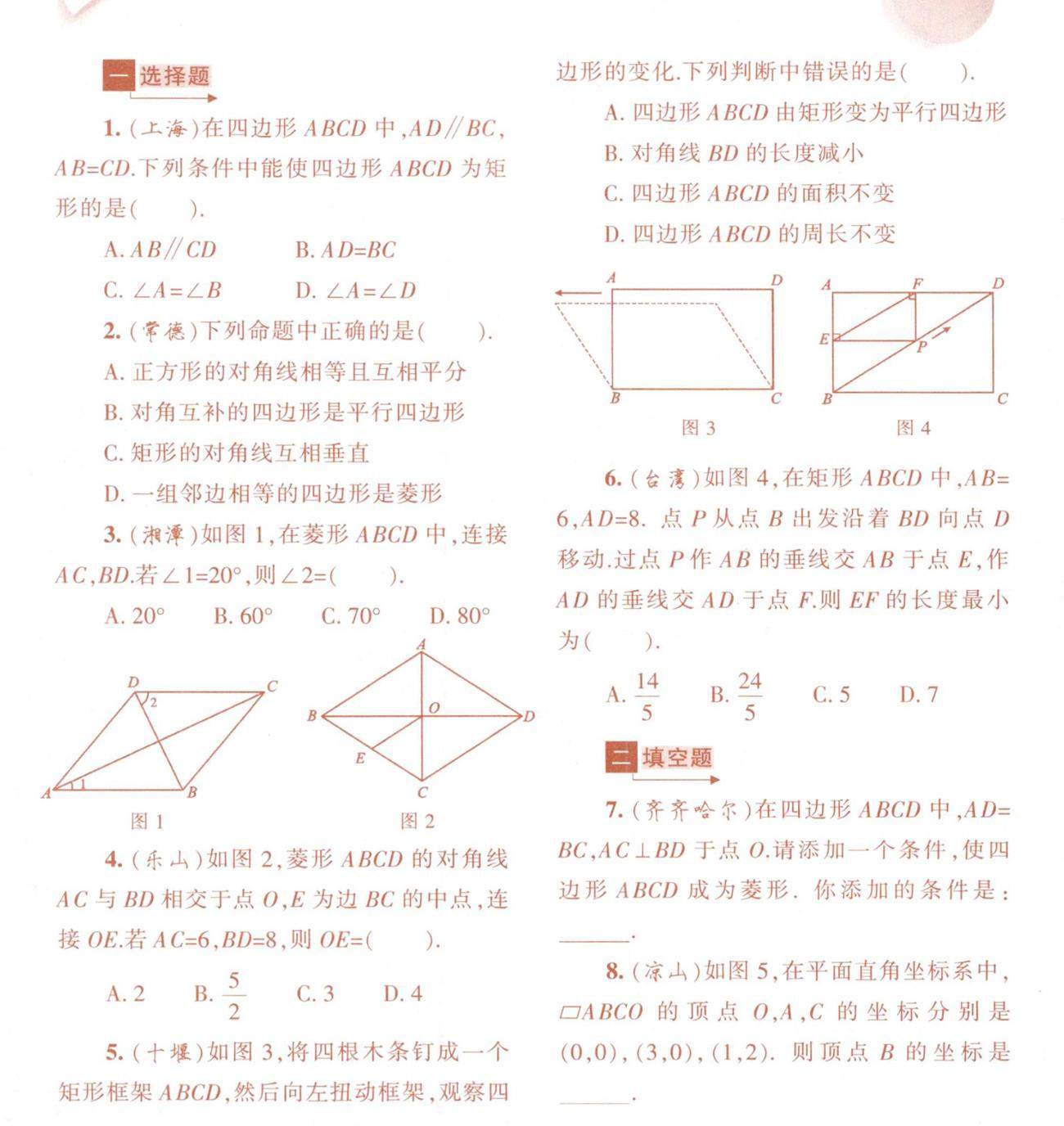
数学之用 | “平行四边形”新题总动员
数学之用 | “平行四边形”新题总动员
-

数学之用 | “平行四边形的性质”基础过关
数学之用 | “平行四边形的性质”基础过关
-

数学之用 | “平行四边形的判定”题型拓展
数学之用 | “平行四边形的判定”题型拓展
-

数学之用 | “特殊的平行四边形”强基固本
数学之用 | “特殊的平行四边形”强基固本
-

数学之用 | “平行四边形”易错题专练
数学之用 | “平行四边形”易错题专练
-

数学之用 | 本期练习类题目参考答案及提示
数学之用 | 本期练习类题目参考答案及提示






















 登录
登录