目录
快速导航-
卷首语 | 一分辛苦一分才
卷首语 | 一分辛苦一分才
-

主编特别推送 | 二次根式的知识要点
主编特别推送 | 二次根式的知识要点
-

专家博客 | 谈二次根式的应用
专家博客 | 谈二次根式的应用
-

名师课堂 | 二次根式有“思想”
名师课堂 | 二次根式有“思想”
-

名师课堂 | 巧用二次根式的非负性
名师课堂 | 巧用二次根式的非负性
-

名师课堂 | 练就火眼金睛 挖出隐含条件
名师课堂 | 练就火眼金睛 挖出隐含条件
-

名师课堂 | 三大对策引领突破根式除法瓶颈
名师课堂 | 三大对策引领突破根式除法瓶颈
-

名师课堂 | 最简二次根式学习三步走
名师课堂 | 最简二次根式学习三步走
-

中考链接 | “二次根式”常考题型归纳
中考链接 | “二次根式”常考题型归纳
-

解题技巧 | 二次根式大小巧比较
解题技巧 | 二次根式大小巧比较
-

解题技巧 | 根式运算有什么技巧
解题技巧 | 根式运算有什么技巧
-

解题技巧 | 八招“降伏”二次根式求值问题
解题技巧 | 八招“降伏”二次根式求值问题
-

马虎不得 | 找出“病因”拔除“病根”
马虎不得 | 找出“病因”拔除“病根”
-

奇趣数学 | 几乎是个整数
奇趣数学 | 几乎是个整数
-
奇趣数学 | 神奇的数字“黑洞”
奇趣数学 | 神奇的数字“黑洞”
-
青春校园 | 和考试焦虑说再见
青春校园 | 和考试焦虑说再见
-
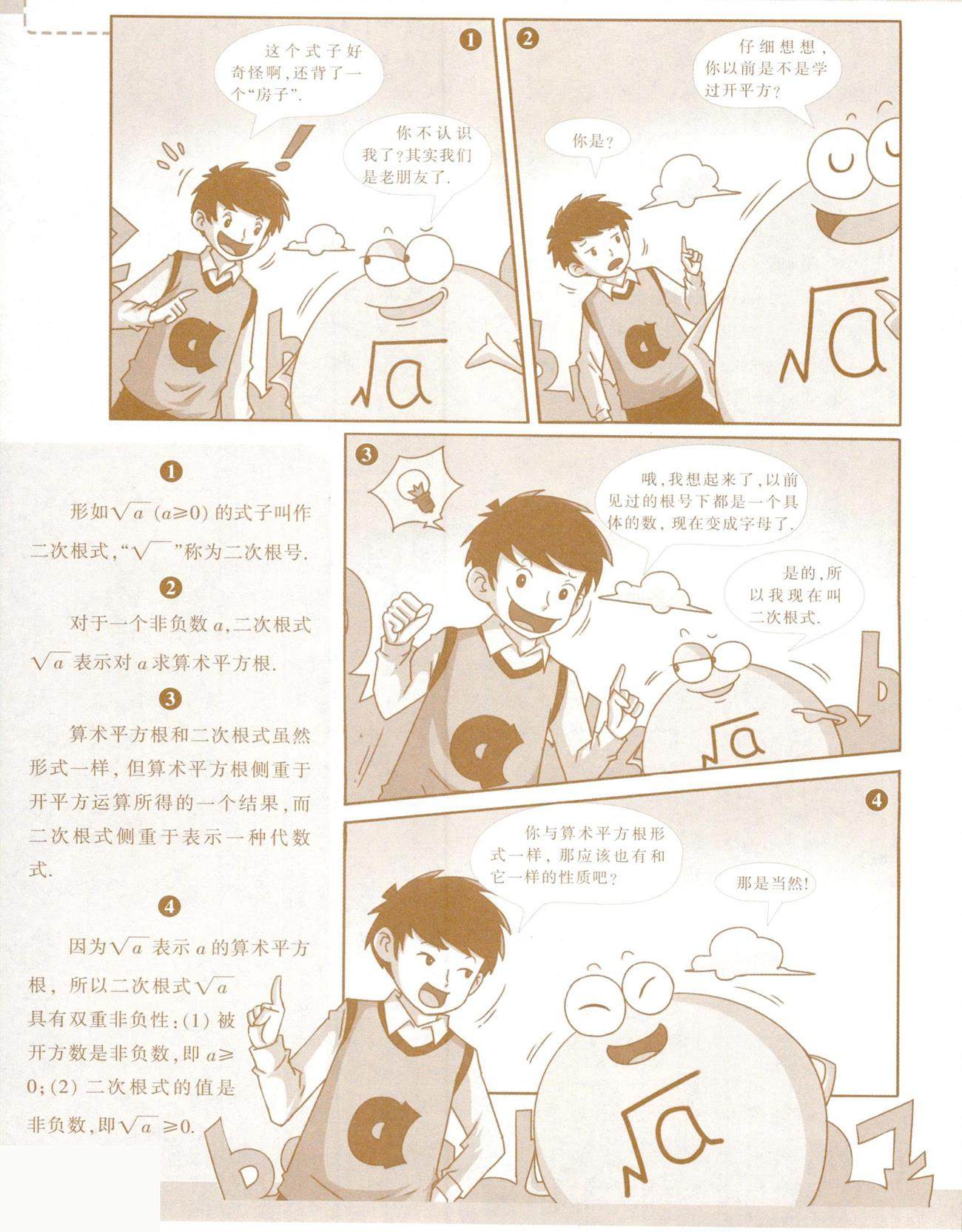
连环画 | 背着“房子”的二次根式
连环画 | 背着“房子”的二次根式
-

竞赛园地 | 数学潜能知识竞赛
竞赛园地 | 数学潜能知识竞赛
-
智慧宫 | 当当闯关记
智慧宫 | 当当闯关记
-

复习点拨 | 多姿多彩的三角形新定义题
复习点拨 | 多姿多彩的三角形新定义题
-

复习点拨 | 先变换 再分解
复习点拨 | 先变换 再分解
-

复习点拨 | 轴对称考点剖析
复习点拨 | 轴对称考点剖析
-

复习点拨 | 因式分解考点扫描
复习点拨 | 因式分解考点扫描
-

复习点拨 | 神通广大的全等三角形
复习点拨 | 神通广大的全等三角形
-

复习点拨 | 关注新题型思维添韧性
复习点拨 | 关注新题型思维添韧性
-

复习点拨 | 分式方程用处大美好生活需要它
复习点拨 | 分式方程用处大美好生活需要它
-

复习点拨 | 巧构等腰三角形
复习点拨 | 巧构等腰三角形
-

复习点拨 | 几何图形中的整式乘法
复习点拨 | 几何图形中的整式乘法
-

能力提升 | “二次根式”新题总动员
能力提升 | “二次根式”新题总动员
-

能力提升 | “二次根式”基础巩固
能力提升 | “二次根式”基础巩固
-

能力提升 | “二次根式的乘除”能力启航
能力提升 | “二次根式的乘除”能力启航
-

能力提升 | “二次根式的加减”题型过关
能力提升 | “二次根式的加减”题型过关
-

能力提升 | “二次根式”易错题
能力提升 | “二次根式”易错题
-

金钥匙 | 本期练习类题目参考答案及提示
金钥匙 | 本期练习类题目参考答案及提示






















 登录
登录