目录
快速导航-
卷首语 | 灵感是“踏遍”的结果
卷首语 | 灵感是“踏遍”的结果
-

数学之基 | 再议轴对称
数学之基 | 再议轴对称
-

数学之基 | 遇等腰勿忘分类讨论
数学之基 | 遇等腰勿忘分类讨论
-

数学之基 | 等腰三角形小魔术
数学之基 | 等腰三角形小魔术
-

数学之基 | 添加辅助线 用好30°角
数学之基 | 添加辅助线 用好30°角
-
数学之基 | “轴对称”考点展播
数学之基 | “轴对称”考点展播
-

数学之基 | 轴对称与三角形的最值问题
数学之基 | 轴对称与三角形的最值问题
-

数学之基 | 都是一知半解惹的“祸”
数学之基 | 都是一知半解惹的“祸”
-

数学之趣 | 俄罗斯方块中的轴对称
数学之趣 | 俄罗斯方块中的轴对称
-

数学之趣 | 当当闯关记
数学之趣 | 当当闯关记
-

数学之趣 | 数学潜能知识竞赛
数学之趣 | 数学潜能知识竞赛
-
数学之趣 | 跟“拖延症”说再见
数学之趣 | 跟“拖延症”说再见
-
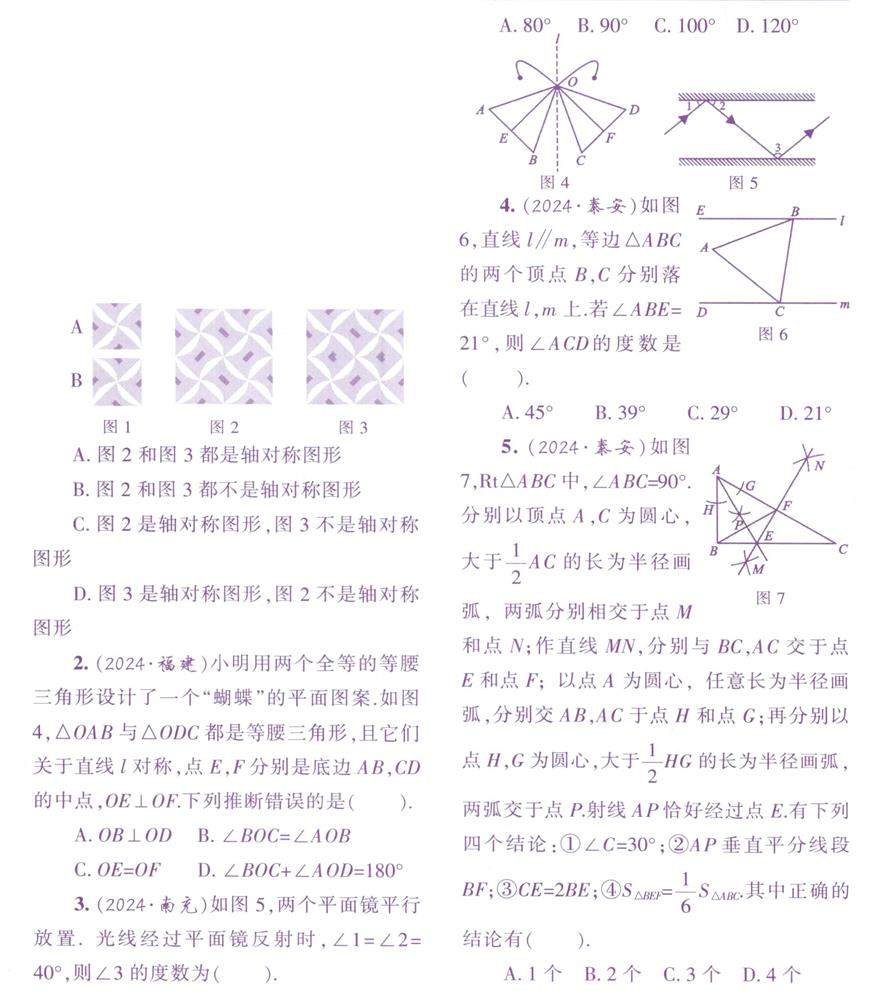
数学之用 | “轴对称”新题总动员
数学之用 | “轴对称”新题总动员
-

数学之用 | “轴对称”基础巩固
数学之用 | “轴对称”基础巩固
-

数学之用 | “画轴对称图形”过关检测
数学之用 | “画轴对称图形”过关检测
-

数学之用 | “等腰三角形”查漏补缺
数学之用 | “等腰三角形”查漏补缺
-

数学之用 | “轴对称”易错题专练
数学之用 | “轴对称”易错题专练
-

数学之用 | 本期练习类题目参考答案及提示
数学之用 | 本期练习类题目参考答案及提示






















 登录
登录